java和c#中的装箱和拆箱操作

c#装箱和拆箱

装箱:整体上来说，装箱是将值类型转换成引用类型，比如将Vector3转换成Object类型。

具体而言：

1）在托管堆中为值类型分配内存。除了原始的数值以外还应该有指向该数值的引用。

2）值类型数据复制到引用类型的堆内存中。

3）再返回对象的引用。

拆箱;一般来说，拆箱是将引用类型转换成值类型，比如将Object类型转换成Vector3类型。

具体而言：

1）首先在托管堆上获取到引用类型的引用。

2）将引用的值类型对象复制到线程栈上。

java装箱和拆箱

装箱：基本数据类型转换为包装器类型，比如将int类型转换为Interger类型。

拆箱：包装器类型转化为基本数据类型，比如将Interger类型转换为int类型。

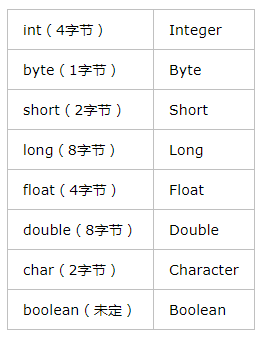
上图上左边是基本数据类型，右边是包装器类型。

装箱是通过调用包装器中的ValueOf()方法，而拆箱是通过调用包装器中的IntValue()方法。

需要强调一点的是：如果在[-128,127]之间，创建的Integer类型指向同一个对象，其值是相同的，而如果超出了这个范围，即使对相同的类型赋予相同的值，其中依旧不同，因为引用不同。

我只想开心充实过好今天，明天以后爱咋咋，爱谁谁！