机器学习入门11 - 逻辑回归 (Logistic Regression)

原文链接：https://developers.google.com/machine-learning/crash-course/logistic-regression/

逻辑回归会生成一个介于 0 到 1 之间（不包括 0 和 1）的概率值，而不是确切地预测结果是 0 还是 1。

1- 计算概率

许多问题需要将概率估算值作为输出。
逻辑回归是一种极其高效的概率计算机制，返回的是概率（输出值始终落在 0 和 1 之间）。
可以通过如下两种方式使用返回的概率：

• “按原样”：“原样”使用返回的概率（例如，用户点击此广告的概率为 0.00023）。
• “转换成二元类别”：将返回的概率转换成二元值（例如，这封电子邮件是垃圾邮件）。

S型函数
S型函数会生成一个介于 0 和 1 之间的值。
定义：
        $y = \frac{1}{1 + e^{-z}}$
曲线图：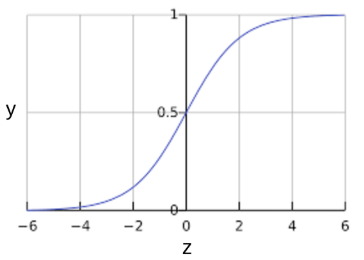

可以看出，S型函数的生成值恰好符合“逻辑回归返回的输出值范围”。
将S型函数应用在机器学习中，用数学方法表示为：
        $y' = \frac{1}{1 + e^{-(z)}}$
其中：

• y' 是逻辑回归模型针对特定样本的输出。
• z 表示使用逻辑回归训练的模型的线性层的输出，是 b + w1x1 + w2x2 + … wNxN
• w 的值是该模型学习的权重，b 是偏差。
• x 的值是特定样本的特征值。

此时，具有机器学习标签的 S 型函数的曲线图：

注意：z 也称为对数几率，因为 S 型函数的反函数表明，z 可定义为标签“1”的概率除以标签“0”的概率得出的值的对数：        $z = log(\frac{y}{1-y})$

2- 模型训练

逻辑回归的损失函数

线性回归的损失函数是平方损失。逻辑回归的损失函数是对数损失函数，定义如下：
        $Log Loss = \sum_{(x,y)\in D} -ylog(y') - (1 - y)log(1 - y')$
其中：

• (xy)ϵD 是包含很多有标签样本 (x,y) 的数据集。
• “y”是有标签样本中的标签。由于这是逻辑回归，因此“y”的每个值必须是 0 或 1。
• “y'”是对于特征集“x”的预测值（介于 0 和 1 之间）。

逻辑回归中的正则化

正则化在逻辑回归建模中极其重要。
如果没有正则化，逻辑回归的渐近性会不断促使损失在高维度空间内达到 0。
因此，大多数逻辑回归模型会使用以下两个策略之一来降低模型复杂性：

• L2 正则化。
• 早停法，即，限制训练步数或学习速率。

假设向每个样本分配一个唯一 ID，且将每个 ID 映射到其自己的特征。
如果未指定正则化函数，模型会变得完全过拟合。
这是因为模型会尝试促使所有样本的损失达到 0 但始终达不到，从而使每个指示器特征的权重接近正无穷或负无穷。
当有大量罕见的特征组合且每个样本中仅一个时，包含特征组合的高维度数据会出现这种情况。

3- 总结

• 逻辑回归模型会生成概率。
• 对数损失函数是逻辑回归的损失函数。
• 逻辑回归被很多从业者广泛使用。

4- 关键词

二元分类 (binary classification)
一种分类任务，可输出两种互斥类别之一。
例如，对电子邮件进行评估并输出“垃圾邮件”或“非垃圾邮件”的机器学习模型就是一个二元分类器。

逻辑回归 (logistic regression)
一种模型，通过将 S 型函数应用于线性预测，生成分类问题中每个可能的离散标签值的概率。
虽然逻辑回归经常用于二元分类问题，但也可用于多类别分类问题（其叫法变为多类别逻辑回归或多项回归）。

S 型函数 (sigmoid function)
一种函数，可将逻辑回归输出或多项回归输出（对数几率）映射到概率，以返回介于 0 到 1 之间的值。
S 型函数的公式如下：
        $y = \frac{1}{1 + e^{-\sigma}}$
在逻辑回归问题中， $\sigma$非常简单：
        $\sigma = b + w_1x_1 + w_2x_2 + … w_nx_n$
换句话说，S 型函数可将  转换为介于 0 到 1 之间的概率。
在某些神经网络中，S 型函数可作为激活函数使用。

早停法 (early stopping)
一种正则化方法，是指在训练损失仍可以继续降低之前结束模型训练。
使用早停法时，您会在验证数据集的损失开始增大（也就是泛化效果变差）时结束模型训练。

对数损失函数 (Log Loss)
二元逻辑回归中使用的损失函数。

L1 正则化 (L₁ regularization)
一种正则化，根据权重的绝对值的总和来惩罚权重。
在依赖稀疏特征的模型中，L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0，从而将这些特征从模型中移除。
与 L2 正则化相对。

L2 正则化 (L₂ regularization)
一种正则化，根据权重的平方和来惩罚权重。
L2 正则化有助于使离群值（具有较大正值或较小负值）权重接近于 0，但又不正好为 0。
（与 L1 正则化相对。）在线性模型中，L2 正则化始终可以改进泛化。