TypeScript算法与数据结构-队列和循环队列

本文涉及的源码，均在我的github。有两部分队列和循环队列。有问题的可以提个issue，看到后第一时间回复

1. 队列(Queue)

队列也是一种线性的数据结构，队列是一种先进先出的数据结构。类似于生活中的排队买东西，先进入队列的人可以先购买到东西。这次的队列具体实现依然会采用之前自己封装好的数组，具体的优势依然是我们可以清晰的算出每次操作的时间复杂度。对于基本的队列而言，主要包含两个基本的操作入队(enqueue)和出队(dequeue)。
对于队列而言，入队发生在尾部，出队发生在首部，队列是一种先进先出的数据结构First in First out。
我们依然会给队列定义一个接口，然队列类实现这个接口

interface Queue<E> {
    getSize(): number; // 获取队列中元素的个数
    isEmpty(): boolean; // 判断队列中的元素是否为空
    enqueue(e: E): void; // 入队一个元素
    dequeue(): E; // 出队一个元素
    getFront(): E; // 获取当前队首的元素
}

1.1 构造函数

这里我们用到了之前封装好的数组

class ArrayQueue<E> implements Queue<E> {
    private array: MyArray<E>;
    constructor(capacity = 10) {
        this.array = new MyArray<E>(capacity);
    }
}

1.2 入队

入队我们只需要将元素添加到array的尾部，这里的时间复杂度为O(1)

enqueue(e: E): void {
    this.array.addLast(e);
}

1.3 出队

出队的话我们需要将元素从array的头部移除，这里的时间复杂度为O(n)。这里为什么需要O(n)的时间复杂度，因为一旦我们要将第一个元素移除，那我们必须遍历整个array，将从位置1开始的每个元素向前移动一个位置。

dequeue(): E {
    return this.array.removeFirst();
}

2.循环队列

循环队列是对队列的一种优化，入队和出队时，在不触发扩容和缩容操作的情况下，均能实现O(1)的时间复杂度。循环队列的原理是利用两个指针，一个指向队列的头部，一个指向队列的尾部。对于循环队列而言我们依然会实现上面的接口。
这里的构造函数会和之前的构造函数有所不同，主要是添加了两个执行队列头元素和队列尾元素的指针，初始状态下，循环队列的头指针和尾指针都

class LoopQueue<E> implements Queue<E> {
    private data: Array<E>;
    private front: number = 0;
    private tail: number = 0;
    private size: number = 0;
    constructor(capacity = 10) {
        this.data = new Array<E>(capacity + 1); // 这里需要在用户传入初始容量的基础上加1
    }
}

2.1 入队

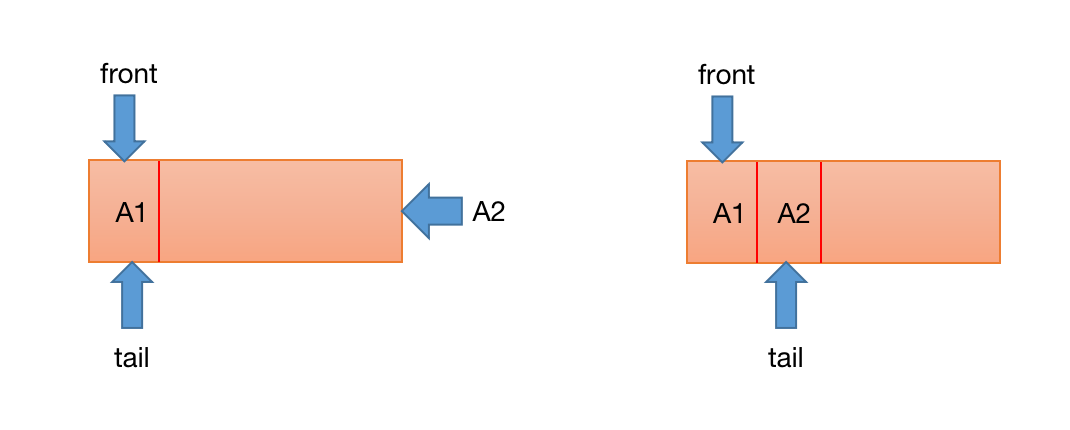
循环队列入队的操作非常简单，将tail节点所指向的节点赋值为所需要添加的节点e，然后维护一下tail指针所指向的位置。这里有一点需要注意的是，当队尾没有空元素时，队列尾指针会循环至队列的头部，然后从头开始。这也就是为什么称之为循环队列。循环队列的入队操作的时间复杂度为O(1)。

enqueue(e: E) {
    // 如果循环队列已满，那此时需要扩容
    if ((this.tail + 1) % this.data.length === this.front) {
        this.resize(this.getCapacity() * 2);
    }
    this.data[this.tail] = e;
    this.tail = (this.tail + 1) % this.data.length;
    this.size++;
}

2.2 出队

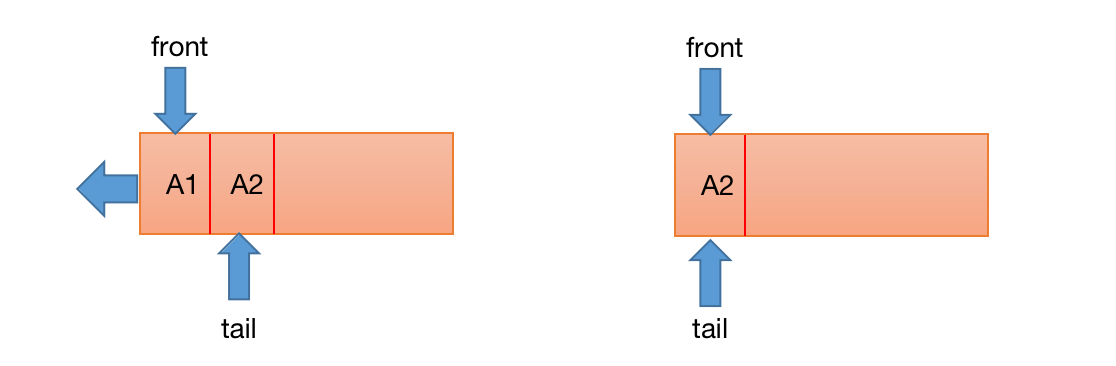
出队的操作和入队相似，将当前front位置的元素置为undefined，然后维护一下front指针的位置。同样的，在不触发缩容操作的情况下，出队操作能保证O(1)的时间复杂度

dequeue(): E {
    if (this.isEmpty()) {
        throw new Error('Cannot dequeue from an empty queue.');
    }

    let ret: E = this.data[this.front];
    this.data[this.front] = undefined;
    this.front = (this.front + 1) % this.data.length;
    this.size--;

    if (this.size === this.getCapacity() / 4 && this.getCapacity() / 2 !== 0) {
        this.resize(this.getCapacity() / 2);
    }

    return ret;
}

2.3 循环队列的优势

循环队列的优势在于

循环队列最大程度的利用的数组的空间，节省内存
循环队列实现了入队和出队的操作都是O(1)的时间复杂度