概率分布的python实现

接上篇概率分布，这篇文章讲概率分布在python的实现。

文中的公式使用LaTex语法，即在\begin{equation}至\end{equation}的内容可以在https://www.codecogs.com/latex/eqneditor.php?lang=zh-cn页面转换出

正确的格式

二项分布(Binomial Distribution)

包含n个相同的试验

每次试验只有两个可能的结果：“成功”或“失败”。

出现成功的概率p对每一次试验是相同的，失败的概率q也是如此，且p+q=1。

试验是互相独立的。

试验成功或失败可以计数，即试验结果对应于一个离散型随机变量。

以X表示n次重复独立试验中事件A(成功)出现的次数，则

\begin{equation}

P{X=x}=C_{n}^{x} p^{x} q^{n-x}, \quad x=0,1,2, \cdots, n

\end{equation}

在python中，可以使用scipy.stats模块中的binom.rvs()方法生成符合二项分布的离散随机变量。该方法的参数n表示n次重复独立试验，p表示事件A出现的次数。size表示做多少次二项分布试验。

同时，本文中使用seaborn的distplot方法绘制随机变量分布的直方图。在大数据量的试验下，通过随机变量出现的频率除以试验的次数，可以得到特定离散随机变量出现的概率。

from scipy.stats import binom
import seaborn as sns
data_binom = binom.rvs(n=10,p=0.5,size=10000)
ax = sns.distplot(data_binom,
                  kde=False,
                  color='green',
                  hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Binomial Distribution', ylabel='Frequency')

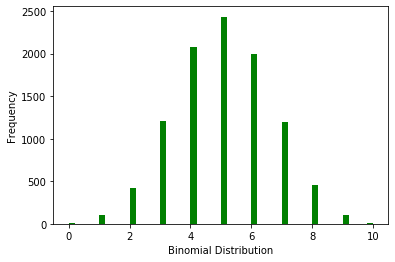
# 可以打印随机变量的值，按照定义，其值为出现A事件的次数，范围肯定在[0,1]
print(data_binom)
[2 3 6 ... 5 4 3]

以抛硬币试验解析上图，得出连续抛10次硬币，5次为正面的概率最高，概率趋近于2500/10000=25%。

贝努里分布(Bernoulli Distribution)

贝努里分布为特殊的二项分布，即每次执行一次试验(n=1)，然后获取单次试验的随机变量的值，为0或1。所以贝努里分布也被称为0-1分布。其分布函数为：

\begin{equation}

P{X=x}=p^{x} q^{1-x}, \quad x=0,1

\end{equation}

在python中，可以使用scipy.stats模块中的bernoulli.rvs()方法生成符合二项分布的离散随机变量。其它参数同二项分布。

from scipy.stats import bernoulli
data_bern = bernoulli.rvs(size=10000,p=0.5)
ax= sns.distplot(data_bern,
                 kde=False,
                 color="green",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Bernoulli Distribution', ylabel='Frequency')

以抛硬币试验解析上图，得出正面和反面出现的概率，趋近于5000/10000=50%。

几何分布(Geometric distribution)

几何分布是指在n次贝努里试验中，经过k次获得1次成功的概率。

 几何分布的特点：
（1）进行一系列相互独立的试验；
（2）每一次试验既有成功的可能，也有失败的可能，且单次试验的成功概率相同；
（3）主要是为了取得第一次成功需要进行多少次试验。

其分布函数为：

\begin{equation}

P{X=k}=p (1-p)^{k-1}, \quad k \geqslant 1

\end{equation}

在python中，可以使用scipy.stats模块中的geom.rvs()方法得出几何分布的离散随机变量。

from scipy.stats import geom
data_geom = geom.rvs(size=10000,p=0.5)
ax= sns.distplot(data_geom,
                 kde=False,
                 color="green",
                 hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Geometric Distribution', ylabel='Frequency')

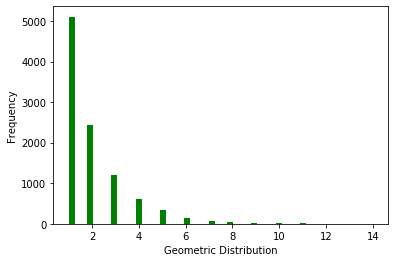
泊松分布(Poisson distribution)

泊松分布是用来描述在一指定时间范围内或在指定的面积或体积之内某一事件出现的次数的分布，例如某企业每月发生事故的次数。

泊松分布的公式为：

\begin{equation}

P(X)=\frac{\lambda^{x} \mathrm{e}^{-\lambda}}{x !}, \quad x=0,1,2, \cdots

\end{equation}

式中，\(\lambda\)为给定的时间间隔内事件的平均数。

在python中，可以使用scipy.stats模块中的poisson.rvs()方法得出泊松分布的连续随机变量。其中参数mu即为公式中的\(\lambda\)，其它参数同上文方法。

from scipy.stats import poisson
data_poisson = poisson.rvs(mu=3, size=10000)
ax = sns.distplot(data_poisson,
                  bins=30,
                  kde=False,
                  color="green",
                  hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Poisson Distribution', ylabel='Frequency')

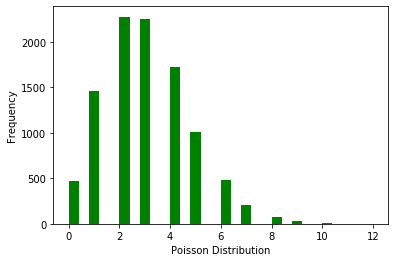
正态分布(Normal Distribution)

在连续型随机变量中，最重要的一种随机变量是具有钟形概率分布的随机变量。人们称它为正态随机变量，相应的概率分布称为正态分布。

如果随机变量X的概率密度为：

\begin{equation}

f(x)=\frac{1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{1}{2 \sigma^{2}}(x-\mu){2}}, \quad-\infty<x<+\infty

\end{equation}

则称X服从正态分布，记作\(X \sim N\left(\mu, \sigma^{2}\right)\)，其中，\(-\infty< \mu <+\infty\)，\(\sigma > 0\), \(\mu\)为随机变量X的均值，\(\sigma​\)为随机变量X的标准差，它们是正态分布的两个参数。

在python中，可以使用scipy.stats模块中的norm.rvs()方法产生符合二项分布的连续随机变量。其中参数loc代表随机变量的均值，size变量代表随机变量的标准差。

from scipy.stats import norm
# 生成标准正态分布，N(0,1)
data_normal = norm.rvs(size=10000,loc=0,scale=1)
ax = sns.distplot(data_normal,
                  bins=100,
                  kde=True,
                  color="green",
                  hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Normal Distribution', ylabel='Frequency')

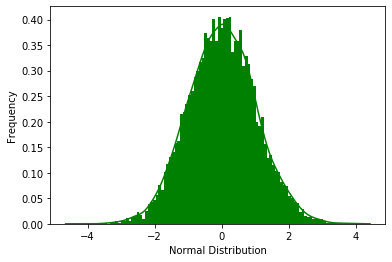
总结

本文通过scipy.stats包中的随机分布函数rvs方法(Random variates)，执行10000次随机变量的计算，通过随机变量值个数直方图的绘制得出特定分布的图形。

另外，也可以通过随机分布函数的pmf方法直接获得指定参数下的概率值，然后画出参数与概率的对应关系，但在本文中不做展开。

欢迎扫描二维码关注公众号