ACM-ICPC 2018 南京赛区网络预赛 B. The writing on the wall

题目链接：https://nanti.jisuanke.com/t/30991

2000ms
262144K

Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 3030 Yuan).

However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.

The wall is covered by square ceramic tiles, which can be regarded as a n * mn∗m grid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.

For example, the following 3 * 33∗3 wall contains 3636 rectangles:

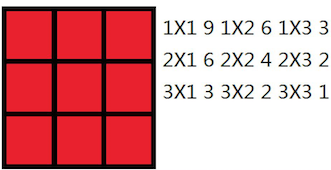
Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.

Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.

Input

There are multiple test cases in the input data.

The first line contains a integer TT : number of test cases. T \le 5T≤5.

For each test case, the first line contains 33 integers n , m , kn,m,k , denoting that the wall is a n \times mn×m grid, and the number of the black tiles is kk.

For the next kk lines, each line contains 22 integers: x\ yx y ,denoting a black tile is on the xx-th row and yy-th column. It's guaranteed that all the positions of the black tiles are distinct.

For all the test cases,

1 \le n \le 10^5,1\le m \le 1001≤n≤105,1≤m≤100,

0 \le k \le 10^5 , 1 \le x \le n, 1 \le y \le m0≤k≤105,1≤x≤n,1≤y≤m.

It's guaranteed that at most 22 test cases satisfy that n \ge 20000n≥20000.

Output

For each test case, print "Case #xx: ansans" (without quotes) in a single line, where xx is the test case number and ansans is the answer for this test case.

Hint

The second test case looks as follows:

样例输入复制

样例输出复制

Case #1: 36

Case #2: 20

题目来源

ACM-ICPC 2018 南京赛区网络预赛

编辑代码

题目大意：输入t，代表t组样例，每组样例包括n,m,k三个数，表示n*m的网格，k个网格是有阴影的，接下来k行，每行包括两个数x,y，表示该阴影矩形的坐标，问你总共有多少个矩形，不算阴影的

思路：遍历n*m矩形的每一个点，把这个点当作矩形的右下角的点，以这个点问矩形的右下角，往左遍历，用一个up 数组存起来该点离顶端的高度，up值的总和即为该点的矩形数。具体看代码：

#include<iostream>

#include<string.h>

#include<map>

#include<cstdio>

#include<cstring>

#include<stdio.h>

#include<cmath>

#include<ctype.h>

#include<math.h>

#include<algorithm>

#include<set>

#include<queue>

typedef long long ll;

using namespace std;

const ll mod=1e9;

const int maxn=1e5+;

const int maxm=1e2+;

const int maxx=1e4+;

const ll maxe=+;

#define INF 0x3f3f3f3f3f3f

#define Lson l,mid,rt<<1

#define Rson mid+1,r,rt<<1|1

int n,m,ca=;

bool a[maxn][maxm];

int up[maxm];

void solve()

{

    ll ans=;

    for(int i=;i<=n;i++)

    {

        for(int j=;j<=m;j++)

        {

            if(a[i][j]) up[j]=;//有阴影，则高度为0

            else up[j]++;//高度的累加

        }

        for(int j=;j<=m;j++)

        {

             int minn=mod;//初值无穷大

             for(int k=j;k>=;k--)//从该点往左遍历

             {

                 minn=min(minn,up[k]);//最小的高度才是真的能构成的矩形数，可以自己在本子上模拟一下

                 ans+=minn;

             }

        }

    }

    printf("Case #%d: %lld\n",ca++,ans);

}

int main()

{

    int t,k,x,y;

    cin>>t;

    while(t--)

    {

        memset(a,false,sizeof(a));//

        memset(up,,sizeof(up));//表示该点到顶端的高度

        cin>>n>>m>>k;

        for(int i=;i<k;i++)

        {

            cin>>x>>y;

            a[x][y]=true;//为true表示该点是阴影的

        }

        solve();

    }

    return ;

}