【51nod1677】treecnt（树上数学题）

点此看题面

大致题意： 给你一个节点从\(1\sim n\)编号的树，让你从中选择\(k\)个节点并通过选择的边联通，且要使选择的边数最少，让你计算对于所有选择\(k\)个节点的情况最小选择边数的总和。

题解

这道题乍一看很麻烦：最短路径？最小生成树？\(LCA\)？通通都不用！！！

其实，这道题就是一道很简单的数学题。

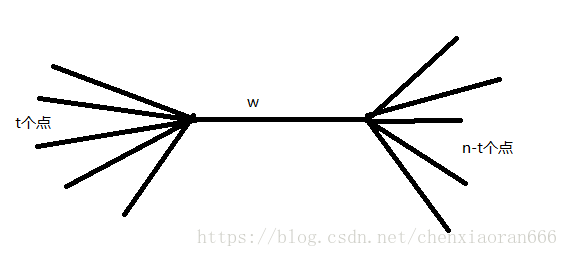
如上图所示，对于某一条边\(w\)，假设它的一边共有\(t\)个节点，则显然它的另一边共有\(n-t\)个节点。

对于一条边的贡献，我们可以这样理解：在多少种情况下，这条边的两边都有被选入\(k\)个点中的点，此时这个点就必须被选。

而对于这些点的分布，有以下三种情况：

①这条边的两边都有点被选，这种情况的可能性就是我们要求的，但是难以直接计算。

②所有被选中的点都在这条边的左面，由于这条边的左边共有\(t\)个点，因此这种情况的可能性为\(C_t^k\)。

③所有被选中的点都在这条边的右面，由于这条边的右边共有\(n-t\)个点，因此这种情况的可能性为\(C_{n-t}^k\)。

由于总情况数为\(C_n^k\)，所以，这条边的两边都有点被选的可能性就是\(C_n^k\) - \(C_t^k\) - \(C_{n-t}^k\)。

既然这样，我们可以直接枚举每一条边，计算出答案并累加即可。

代码

#include<bits/stdc++.h>
#define LL long long
#define N 100000
#define MOD 1000000007
using namespace std;
int n,k,ee=0,lnk[N+5],vis[N+5]={0};
struct edge
{
	int to,nxt,val;
}e[2*N+5];
LL ans=0,fac[N+5]={0},inv[N+5]={0};
inline char tc()
{
	static char ff[100000],*A=ff,*B=ff;
	return A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0;int f=1;char ch;
	while(!isdigit(ch=tc())) if(ch=='-') f=-1;
	while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
	x*=f;
}
inline void write(int x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
inline void add(int x,int y)
{
	e[++ee]=(edge){y,lnk[x],0},lnk[x]=ee;
}
inline LL quick_pow(LL x,LL y)//快速幂
{
	LL res=1;
	while(y)
	{
		if(y&1) (res*=x)%=MOD;
		(x*=x)%=MOD,y>>=1;
	}
	return res;
}
inline void Init()//初始化
{
	register int i;fac[1]=1;
	for(i=2;i<=N+4;++i) fac[i]=(fac[i-1]*i)%MOD;//预处理阶乘
	inv[N+4]=quick_pow(fac[N+4],MOD-2);
	for(i=N+3;i>=0;--i) inv[i]=(inv[i+1]*(i+1))%MOD;//预处理逆元
}
inline LL C(LL x,LL y)//组合数
{
	if(x<y) return 0;
	if(!y) return 1;
	return fac[x]*inv[y]%MOD*inv[x-y]%MOD;
}
inline int dfs(int x)
{
	register int i;LL res=1;vis[x]=1;
	for(i=lnk[x];i;i=e[i].nxt)
	{
		if(!vis[e[i].to])
		{
			LL t=dfs(e[i].to);
			(ans+=C(n,k)%MOD-C(t,k)%MOD-C(n-t,k)%MOD+MOD)%=MOD;//核心计算公式
			res+=t;
		}
	}
	return res;//res表示该边某一侧的点数
}
int main()
{
	register int i;int x,y;
	for(read(n),read(k),i=1;i<n;++i)
		read(x),read(y),add(x,y),add(y,x);
	Init(),dfs(1);
	return write((ans+MOD)%MOD),0;
}