隐型马尔科夫模型(HMM)向前算法实例讲解(暴力求解+代码实现)---盒子模型

先来解释一下HMM的向前算法：

　　前向后向算法是前向算法和后向算法的统称，这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。

　　前向算法本质上属于动态规划的算法，也就是我们要通过找到局部状态递推的公式，这样一步步的从子问题的最优解拓展到整个问题的最优解。在这里我们认为随机过程中各个状态St的概率分布，只与它的前一个状态St-1有关，同时任何时刻的观察状态只仅仅依赖于当前时刻的隐藏状态。

　　在t时刻我们定义观察状态的概率为：

　　　　　　　　　　　　　　　　αt(i)=P(o1,o2,...ot,it=qi|λ)

　　从下图可以看出，我们可以基于时刻t时各个隐藏状态的前向概率，再乘以对应的状态转移概率，即α_t(j)a_ji就是在时刻t观测到o₁,o₂,...o_t，即时刻t隐藏状态q_j,q_j总和再乘以该时刻的发射概率得到时刻t+1隐藏状态q_i的概率。

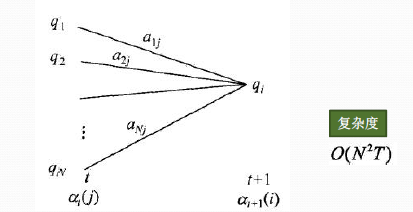
　下面总结下前向算法。

　　　　输入：HMM模型λ=(A,B,Π)λ=(A,B,Π)，观测序列O=(o₁,o₂,...o_T)

　　　　输出：观测序列概率P(O|λ)

　　　　1) 计算时刻1的各个隐藏状态前向概率：

　　　　　　α₁(i)=π_ib_i(o₁),i=1,2,...N

　　　　2) 递推时刻2,3,...T时刻的前向概率：

　　　　　　

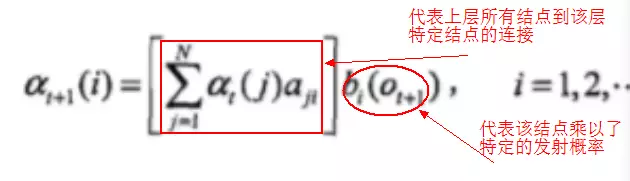
　　　　3) 计算最终结果：

　　　　　　

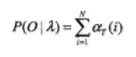
　　　　从递推公式可以看出，我们的算法时间复杂度是O(TN²)，比暴力解法的时间复杂度O(TN^T)少了几个数量级。

实例说明：

3个盒子，每个盒子都有红、白两种球，具体情况如下：

　　　　盒子          1　　 2　　3

　　　　红球数      5　　4　　 7

　　　　黑球数      5　　6　　 3

　　　按照下面的方法从盒子里抽球，开始的时候，从第一个盒子抽球的概率是0.2，从第二个盒子抽球的概率是0.4，从第三个盒子抽球的概率是0.4。以这个概率抽一次球后，将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是：如果当前抽球的盒子是第一个盒子，则以0.5的概率仍然留在第一个盒子继续抽球，以0.2的概率去第二个盒子抽球，以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子，则以0.5的概率仍然留在第二个盒子继续抽球，以0.3的概率去第一个盒子抽球，以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子，则以0.5的概率仍然留在第三个盒子继续抽球，以0.2的概率去第一个盒子抽球，以0.3的概率去第二个盒子抽球。如此下去，直到重复三次，得到一个球的颜色的观测序列:

　　　　　　　　　　　　　　　　　　O={红，白，红}

　　注意在这个过程中，观察者只能看到球的颜色序列，却不能看到球是从哪个盒子里取出的。

如下图：

根据HMM的定义，我们可以得到观察集合：

　　　　　　　　　　　　V=｛红、白｝ M=2

隐藏的状态是：

　　　　　　　　Q=｛盒子1、盒子2、盒子3｝ N=3

而观察序列和状态序列的长度为3.

 

对应的矩阵表示为：

初始状态序列：

　　　　　　　　∏={0.2.0.4.0.4}^T

状态转移矩阵：

　　　　　　   　|0.5　　0.2　　0.3|

　　　　　　A=  |0.3　　0.5　　0.2|

　　　　　　　   |0.2　　0.3　　0.5|

观察状态矩阵：

　　　　　　   　|0.5　　0.5|

　　　　　　B=  |0.4　　0.6|

　　　　　　　   |0.7　　0.3|

1、暴力求解：

 　　①红色球

　　　　　　隐藏状态是盒子1:α1(1)=π1b1(o1)=0.2×0.5=0.1

　　　　　　隐藏状态是盒子2:α1(2)=π2b2(o1)=0.4×0.4=0.16

　　　　　　隐藏状态是盒子3:α1(3)=π3b3(o1)=0.4×0.7=0.28

　　②第一次红色球前提下第二次白色球

　　　　　　　　隐藏状态是盒子1:α2(1)=[0.1∗0.5+0.16∗0.3+0.28∗0.2]×0.5=0.077

　　　　　　隐藏状态是盒子2:α2(2)=[0.1∗0.2+0.16∗0.5+0.28∗0.3]×0.6=0.1104

　　　　　　隐藏状态是盒子3:α2(3)=[0.1∗0.3+0.16∗0.2+0.28∗0.5]×0.3=0.0606

　　③第一次红色球、第二次白色球且第三次红色球

　　　　　　隐藏状态是盒子1:α3(1)=[0.077∗0.5+0.1104∗0.3+0.0606∗0.2]×0.5=0.04187

　　　　　　 隐藏状态是盒子2:α3(2)=[0.077∗0.2+0.1104∗0.5+0.0606∗0.3]×0.4=0.03551

　　　　　　隐藏状态是盒子3:α3(3)=[0.077∗0.3+0.1104∗0.2+0.0606∗0.5]×0.7=0.05284

最终我们求出观测序列:O={红，白，红}的概率为：

　　　　　　P=0.04187+0.03551+0.05284=0.13022

 

1、python代码实现：

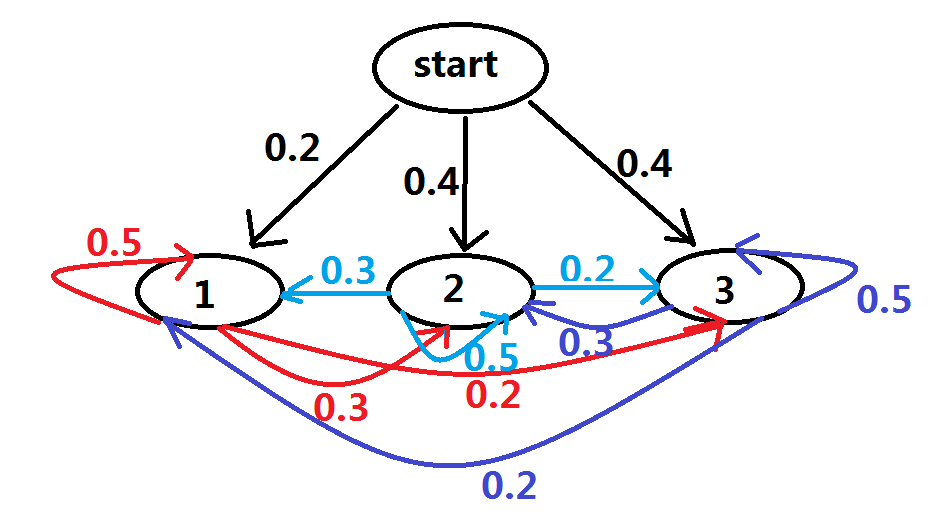
# -*- coding: UTF-8 -*-
import numpy as np
def Forward(trainsition_probability,emission_probability,pi,obs_seq):
    """
    :param trainsition_probability:trainsition_probability是状态转移矩阵
    :param emission_probability: emission_probability是发射矩阵
    :param pi: pi是初始状态概率
    :param obs_seq: obs_seq是观察状态序列
    :return: 返回结果
    """
    trainsition_probability = np.array(trainsition_probability)
    emission_probability  = np.array(emission_probability)

    pi = np.array(pi)
    Row = np.array(trainsition_probability).shape[0]

    F = np.zeros((Row,Col))                      #最后要返回的就是F，就是我们公式中的alpha
    F[:,0] = pi * np.transpose(emission_probability[:,obs_seq[0]])  #这是初始化求第一列,就是初始的概率*各自的发射概率
    for t in range(1,len(obs_seq)):              #这里相当于填矩阵的元素值
        for n in range(Row):                     #n是代表隐藏状态的
            F[n,t] = np.dot(F[:,t-1],trainsition_probability[:,n])*emission_probability[n,obs_seq[t]]   #对应于公式,前面是对应相乘
    return F

if __name__ == '__main__':
    trainsition_probability = [[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]]
    emission_probability = [[0.5,0.5],[0.4,0.6],[0.7,0.3]]
    pi = [0.2,0.4,0.4]

    #然后下面先得到前向算法,在A,B,pi参数已知的前提下，求出特定观察序列的概率是多少?
    obs_seq = [0,1,0]
    Row = np.array(trainsition_probability).shape[0]
    Col = len(obs_seq)

    F = Forward(trainsition_probability,emission_probability,pi,obs_seq)
    print F

对应结果：

[[ 0.1  　　 0.077 　　   0.04187 ]
[ 0.16 　　 0.1104 　　 0.035512]
[ 0.28 　　 0.0606 　　 0.052836]]

 

 

参考文章：隐马尔科夫模型HMM（二）前向后向算法评估观察序列概率、隐马尔科夫模型-前向算法