组合数学及其应用——polya计数

在处理类似下面的问题中，一般的计数方法会出现问题：假如你要用红、蓝两种颜色给一个正四面体的四个顶点着色，试问存在多少种不同的着色方案？

在高中我们常用的方法是模拟涂色过程，分情况讨论，然后基于分步乘法原理。但是在那里没有考虑几何体通过旋转等操作带来的对称性，在本文中，我们就来介绍一种专门处理这类问题的工具——Polya计数。

首先我们要做的是引入一些基本的概念。

置换：

关于置换更多的细节我们在《抽象代数基础教程》中继续讨论，这里我们只需简单的了解其概念即可。

关于置换还需要了解的就是它的合乘运算。

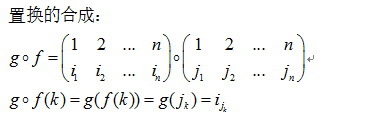
置换这个工具可以方便我们符号化图形的对称分析过程，下面给出要给非常简单的例子，以帮助理解置换如何描述几何体的对称。

考察如下的正方形。

(一个正方形，四个顶点为1234)

我们需要去思考，如何利用置换来描述那些运动，使得正方形位置没变(但是对应标号的顶点可能发生了移动)。

容易看到符合要求的运动有两类。

1)  将正方形绕中心旋转(取顺时针即可)0°、90°、180°、270°.

2)  将正方形按照两条对角线和两条对边中点连线，立体得翻转180°。

那么我们可以发现运动前的正方形顶点序号和运动后的，其实就形成了一个置换。

此时我们开始给出染色方案的数学描述。

基于以上的铺垫，我们可以给出Burnside引理，用于给出一个计数非等价着色数的公式。

在给出Burnside定理之后，我们下面结合几个简单的题目，来加强对这个定理的理解。

问题到这里，就得到很大的改观，之前我们需要基于置换群和着色集合，进行遍历考察来计算Burnside定理和式的一般项，而现在我们只需要，分析置换群G中的每个置换，然后结合颜色数，就可以进行计算了。

我们还需要进一步努力，因为从定理4可以看到，我们用k种颜色形成着色集合，是没有显示颜色的出现次数的，而如果规定某种颜色的出现的次数，我们应该如何处理呢？

最后我们给出立方体的非等价的染色分析，在一般带的考察polya的题目中容易考察但是其对称群较为繁冗容易出错，因此最好一次分析之后记住结论。

例子(立方体的顶点与面的着色)：

用制定数量的颜色对立方体的顶点和面进行着色，尝试求立方体的对称群和非等价的着色方案数目。

考察立方体的对称操作，它们一共可分为如下的四种类型共24种对称：

(1) 恒等对称1个。

(2) 固定一对对立面进行旋转：

(a)90°

(b)180°

(c)270°

由于共有三对对立面，所以上面各有3个共9个。

(3) 绕一对对边重点连线旋转180°，由于有6对，这里有6个对称。

(4) 绕对顶点进行旋转：

(a)120°

(b)240°

可以看到一个立方体的对称群友24个置换，下面我们只需要考察每个置换f的type(f)，以期得到立方体的非等价染色的生成函数。

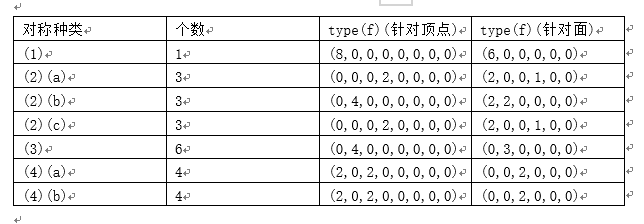
同理我们可以对面对称群进行完全一样的讨论，结果如下：