NYOJ104-最大和-（前缀和）

题意：给一个矩阵，每个元素有正有负，求最大矩阵和。

解题：

（1）对原矩阵a用前缀和处理，处理变成矩阵sum，sum[i][j]表示从左上角为a[1][1]到右下角a[i][j]的全部元素和。

矩阵必须是连续起来的，两重循环列举所有的连续的行，再暴力循环每一列，相当于求最大连续子序列。

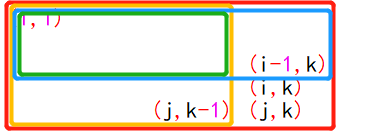
第i行到第j行的第k列压缩成一个数：sum[j][k]-sum[j][k-1]-sum[i-1][k]+sum[i-1][k-1];

图示：红色-黄色-蓝色+绿色

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<string>
#include<vector>
#include<iostream>
#include<cstring>
#include<queue>
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;

int a[105][105];
int sum[105][105];
int t,n,m;

int part(int i,int j,int k)///第i行到第j行在第k列上的和
{
    return sum[j][k]-sum[j][k-1]-sum[i-1][k]+sum[i-1][k-1];
}

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        memset(a,0,sizeof(a));
        memset(sum,0,sizeof(sum));
        scanf("%d %d",&n,&m);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];///初始化矩阵前缀和

        int maxx=-inf;
        int x,y;
        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=n;j++)
            {
                x=part(i,j,1);  ///初始值为第i行到第j行的第1列
                y=x;            ///存两个变量，备份，x拿来操作
                for(int k=2;k<=m;k++)
                {
                    if(x<0)     ///x是从第1列进来的，如果当前的x小于0，越加越小， 不如不加，置为0再加相当于没加
                        x=0;
                    x+=part(i,j,k);///对于 加不加 第i行到第j行的第k列的部分和 ，y对每个x取最值，保存
                    y=max(x,y);
                }
                maxx=max(maxx,y);
            }
        }
        printf("%d\n",maxx);
    }

    return 0;
}

矩阵形式的前缀和

（2）对每一列前缀和处理，sum[i][j]表示a[1][j]到a[i][j]的和，双重暴力连续的行数，一重暴力列数，每个子列，第i行到第j行的第k列压缩成一个数：sum[j][k]-sum[i-1][k]，相当于求最大连续子序列。

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<string>
#include<vector>
#include<iostream>
#include<set>
#include<cstring>
#include<queue>
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;

int a[105][105];
int sum[105][105];
int t,n,m;

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        memset(a,0,sizeof(a));
        memset(sum,0,sizeof(sum));
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                scanf("%d",&a[i][j]);
                sum[i][j]=sum[i-1][j]+a[i][j];///列的前缀和
            }
        }
        int ans=-inf;
        int now,maxx;
        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=n;j++)
            {
                now=sum[j][1]-sum[i-1][1];
                maxx=now;
                for(int k=2;k<=m;k++)
                {
                    if(now<0)
                        now=0;
                    now+=sum[j][k]-sum[i-1][k];
                    maxx=max(now,maxx);
                }
                ans=max(maxx,ans);
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

每列前缀和的形式