信息学奥赛一本通 提高篇 序列第k个数 及 快速幂

我是传送门

这个题首先是先判断是等差还是等比数列

等差的话非常简单:

前后两个数是等差的,举个栗子:

3 6 9 12

这几个数,(我感觉 1 2 3 4并说明不了什么)

每次都加3嘛,很容易看出,第一个数是3 * 1,第二个是3 * 2....以此类推

第k个数 = (第2个数 - 第1个数) * k ;

(z - y) * k % 

% 200907 的原因是题目要求

但是这样并不能过

hack一下

4 7 10 13

用原先的公式:
(7 - 4) * 4 % 200907 = 12;

明显不对啊

但是我们将序列每个都减一

就变成了: 3 6 9 12

熟悉滴感觉,但我们并不需要真的都减一,只需要加上差就可以了

x + (z - y) * (k - ) % 

这个和我说的有些出入,但仔细想想就会发现是一样的

等比的话稍微难一点:

前后两个数是等比的,举个栗子:

3 6 18 27

第一个数是3^1

第二个数是3^2

第三个数是3^3

emmm,好像也很简单

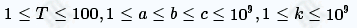
这数据 不能乘10^9次吧

100000000000000% 超时

快速幂不错

快速幂怎么写呢

我在这里说一种非递归写法(其实本蒟蒻根本不明白递归的实现)

把幂次拆成二进制数,只需要乘log n 次,非常优秀的算法

比如 2 ^ 10 的二进制是 2的1010次幂

ans 就是  2 ^ 2 * 2 ^ 8 ;

当然数学上来讲  2 ^ 2 * 2 ^ 8 = 2 ^ (2 + 10)

long long ksm(long long a,long long b,long long n){//a是底数,b是幂数,n是mod数
    long long ans = ;
    while(b){//等价于while(b != 0) ,dalao勿喷,讲给我这样的蒟蒻听
        if ( b & ){//b & 1 等价于 b % 2 == 1
            ans *= a;//是的话乘起来
            ans %= ;//随时取膜性质
            /* code */
        }
        a *= a;//下一位
        a %= ;//膜
        b >>= ;//右移一位  等价于 b /= 2;
    }
    return ans % ;
}

然后问题还是来了

20 920 42320

这个显然是等比数列920 : 20 = 46

但是怎么用快速幂呢

20 = 1 * 20

920 = 46 * 20

42320 = 46 * 46 * 20

那么20 920 42320 和1 45 2025什么区别呢

就是前者每一项是后者20倍

求出后者就能求出前者啦

这个代码不需要解释了吧

#include <bits/stdc++.h>
using namespace std;
long long ksm(long long a,long long b,long long n){
    long long ans = ;
    while(b){
        if ( b & ){
            ans *= a;
            ans %= ;
            /* code */
        }
        a *= a;
        a %= ;
        b >>= ;
    }
    return ans % ;
}

int main()
{
    long long n;
    cin>>n;
    for (long long i = ; i < n; ++i)
    {
        long long x, y, z, k;
        cin>>x>>y>>z>>k;
        if (z - y == y - x)
        {
            cout<<x + (z - y) * (k - ) % <<endl;
            /* code */
        }
        else{
            long long yy = k /  * ;
            yy  /= x;
            yy *= y % ;
            cout/*<<y / x<<' '<<k - 1<<" "*/<<ksm(y / x , k -  , )  * x % <<endl;
//            cout<<ppw(x , yy , 200907 , k , y / x)<<endl;
        }
        /* code */
    }
    return ;
}