【matlab】 QR分解 求矩阵的特征值

"QR_H.m"

function [Q,R] = QR_tao(A)
%输入矩阵A
%输出正交矩阵Q和上三角矩阵R
[n,n]=size(A);
E = eye(n);
X = zeros(n,);
R = zeros(n);

P1 = E;
for k=:n-
    s = -sign(A(k,k))*norm(A(k:n,k));
    R(k,k) = -s;
    if k ==
        w = [A(,)+s,A(:n,k)']';
    else
        w = [zeros(,k-),A(k,k)+s,A(k+:n,k)']';
        R(:k-,k) = A(:k-,k);
    end
    if norm(w)~=
        w = w/norm(w);
    end
    P = E-*w*w';
    A = P*A;
    P1 = P*P1;
    R(:n,n) = A(:n,n);
end

之后根据算法:

An = Q1*R1;

An+1 =  R1*Q1

重复迭代即可。

"QR.m"

%输入 矩阵A 和迭代次数 it_max
%输出 最后对角线上元素为特征值的矩阵
function [Q] = QR(A,it_max)
A1 = A;
for N=:it_max
[Q1,R1] = QR_tao(A1);
A2 = R1*Q1;
A1 = A2;
end
Q=A1

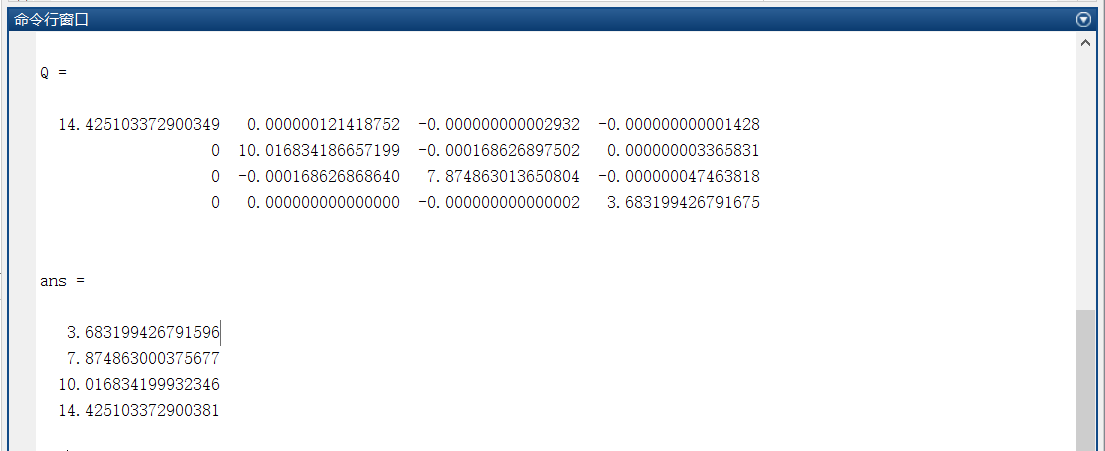
测试： 计算一个矩阵的特征值:

A = [,-,-,;
    -,,,-;
    -,,,-;
    ,-,-,;
];
[Q] = QR(A,)
eig(A)

最后结果: