【算法34】蓄水池抽样算法 (Reservoir Sampling Algorithm)

蓄水池抽样算法简介

蓄水池抽样算法随机算法的一种，用来从 N 个样本中随机选择 K 个样本，其中 N 非常大（以至于 N 个样本不能同时放入内存）或者 N 是一个未知数。其时间复杂度为 O(N),包含下列步骤 (假设有一维数组 S, 长度未知，需要从中随机选择 k 个元素, 数组下标从 1 开始), 伪代码如下:

 array R[k];    // result
 integer i, j;

 // fill the reservoir array
 for each i in  to k do
     R[i] := S[i]
 done;

 // replace elements with gradually decreasing probability
 for each i in k+ to length(S) do
     j := random(, i);   // important: inclusive range
     if j <= k then
         R[j] := S[i]
     fi
 done

算法首先创建一个长度为 k 的数组（蓄水池）用来存放结果，初始化为 S 的前 k 个元素。然后从 k+1 个元素开始迭代直到数组结束，在 S 的第 i 个元素，算法生成一个随机数 $j \in [1, i]$， 如果 j <= k， 那么蓄水池的第 j 个元素被替换为 S 的第 i 个元素。

算法的正确性证明

定理：该算法保证每个元素以 k / n 的概率被选入蓄水池数组。

证明：首先，对于任意的 i，第 i 个元素进入蓄水池的概率为 k / i；而在蓄水池内每个元素被替换的概率为 1 / k; 因此在第 i 轮第j个元素被替换的概率为 (k / i ) * (1 / k) = 1 / i。 接下来用数学归纳法来证明，当循环结束时每个元素进入蓄水池的概率为 k / n.

假设在 (i-1) 次迭代后，任意一个元素进入 蓄水池的概率为 k / (i-1)。有上面的结论，在第 i 次迭代时，该元素被替换的概率为 1 / i， 那么其不被替换的概率则为 1 - 1/i = (i-1)/i；在第i 此迭代后，该元素在蓄水池内的概率为 k / (i-1) * (i-1)/i = k / i. 归纳部分结束。

因此当循环结束时，每个元素进入蓄水池的概率为 k / n. 命题得证。

算法的C++实现

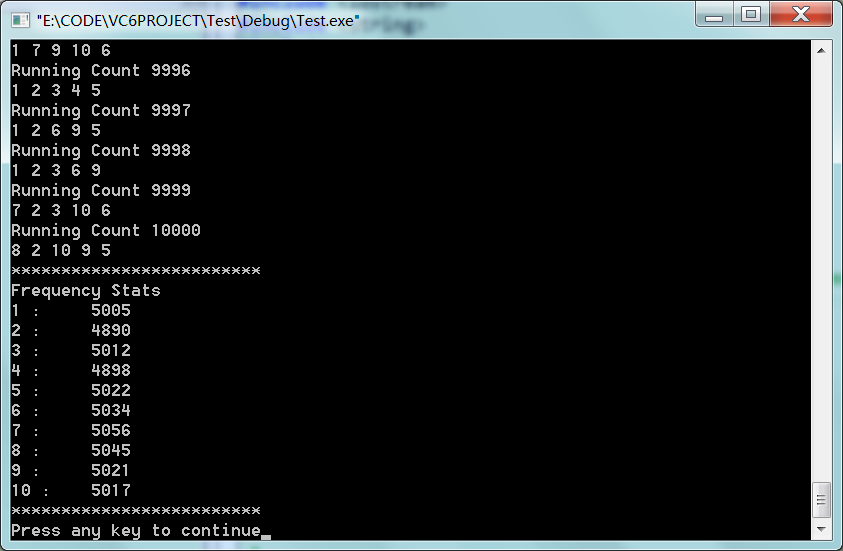
实现部分比较简单，关键点也有详细的注释，为了验证算法的正确性，对[1,10]的数组，随机选择前五个进行验证，运行10000次后，每个数字出现的频率应该是基本相等的，算法的运行结果也证实了这一点，如下图所示。

 #include <iostream>
 #include <string>
 #include <vector>
 #include <cassert>
 #include <cstdio>
 #include <cstdlib>
 #include <ctime>
 using namespace std;

 /**
  * Reservoir Sampling Algorithm
  *
  * Description: Randomly choose k elements from n elements ( n usually is large
  *              enough so that the full n elements may not fill into main memory)
  * Parameters:
  *      v - the original array with n elements
  *      n - the length of v
  *      k - the number of choosen elements
  *
  * Returns:
  *      An array with k elements choosen from v
  *
  * Assert:
  *      k <= n
  *
  * Author:  python27
  * Date:    2015/07/14
  */
 vector<int> ReservoirSampling(vector<int> v, int n, int k)
 {
     assert(v.size() == n && k <= n);

     // init: fill the first k elems into reservoir
     vector<int> reservoirArray(v.begin(), v.begin() + k);

     int i = ;
     int j = ;
     // start from the (k+1)th element to replace
     for (i = k; i < n; ++i)
     {
         j = rand() % (i + ); // inclusive range [0, i]
         if (j < k)
         {
             reservoirArray[j] = v[i];
         }
     }

     return reservoirArray;
 }

 int main()
 {
     vector<int> v(, );
     for (int i = ; i < ; ++i) v[i] = i + ;

     srand((unsigned int)time(NULL));
     // test algorithm RUN_COUNT times
     const int RUN_COUNT = ;
     int cnt[] = {};
     for (int k = ; k <= RUN_COUNT; ++k)
     {
         cout << "Running Count " << k << endl;

         vector<int> samples = ReservoirSampling(v, , );

         for (size_t i = ; i <samples.size(); ++i)
         {
             cout << samples[i] << " ";
             cnt[samples[i]]++;
         }
         cout << endl;
     }

     // output frequency stats
     cout << "*************************" << endl;
     cout << "Frequency Stats" << endl;
     for (int num = ; num < ; ++num)
     {
         cout << num << " : \t" << cnt[num] << endl;
     }
     cout << "*************************" << endl;

     return ;
 }

运行结果如下:

算法的局限性

蓄水池算法的基本假设是总的样本数很多，不能放入内存，暗示了选择的样本数 k 是一个与 n 无关的常数。然而在实际的应用中，k 常常与 n 相关，比如我们想要随机选择1/3 的样本 (k = n / 3)，这时候就需要别的算法或者分布式的算法。

参考文献

【1】 Wikipedia：Reservoir Sampling