AtCoder Regular Contest 091&092

091E(构造)

题意：

　　给出n,a,b。你需要构造出一个长度为n的n的排列，其中最长上升子序列的长度为a，最长下降子序列的长度为b。

　　n,a,,b<=3e5

分析：

　　

　　我们可以构造出这样的数列，容易发现，a和b能表示出的最大的n是ab，能表示出的最小的n是a+b-1，所以只有a+b-1<=n<=ab的才是合法的。

091F(博弈论)

题意：

　　有n堆石子，每堆石子数量是ai，有一个属性ki，一个人取第i堆石子，可以取[1,floor(ai/ki)]个石子。

　　Alice和Bob轮流操作，不能操作的人输，问是否先手必胜。

　　n<=200;ai,ki<=1e9

分析：

　　首先我们可以分析一堆石子，然后把每堆石子的sg异或起来就行了，主要是如何求sg函数

　　可以找到关于sg函数的规律：

　　

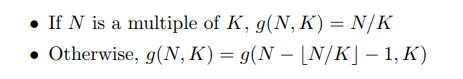
　　然后就是求解sg函数的值了，如果直接按照这个公式去迭代那么会TLE

　　我们可以去枚举[n/k]的值，将n/k相同的一起减掉，我们现在来分析复杂度

　　n/k的值是递减的，所以这部分的复杂度是O(n/k)

　　然后因为可以近似看成n=n-n/k-1，所以n=(k-1/k)n

　　所以每一步n都缩小了1/k

　　因为lim((k-1)/k)^k=1/e，所以可以当作是每k步n的值变成原来的log倍

　　所以n缩小的时间复杂度是O(klogn)

　　所以总的复杂度应该是这两部分时间复杂度的最小值，所以是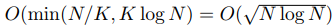

092D(计数)

题意：

　　有两个长度为n的数组a[1..n],b[1..n]，对于每对(i,j),求a[i]+b[j]，把n^2个结果异或起来，求最后的异或的结果。

　　n<=200000,ai,bi<=2^28

分析：

　　考虑对结果的每一位独立考虑，考虑结果的第k位是0还是1

　　对于一个k，关键就是要求有多少个(i,j)满足a[i]+b[j]的第k位是1，如果是奇数个那么答案的第k位就是1否则就是0

　　检测第k位的最常用技巧是&(1<<k)，但&没有分配律所以不行，但我们还有另一个办法，那就是取模

　　设T=2^k,我们考虑(ai+bj)%2T，如果这个数在[T,2T)之间，那么ai+bj的第k位就是1，那么我们如何去统计呢？

　　不妨先把a和b的所有数都对2T取模，然后其实就是T<=ai+bj<2T 或者 3T<=ai+bj<4T

　　排序+二分去统计就行了

　　时间复杂度O(nlognlogc)

092E(构造)

题意：

　　

分析：

　　最终的结果一定是某些位置上的数字的和，且这些数字的下标位置是同奇偶的

　　于是我们可以对于奇数位置和偶数位置分别去求个最大的和，比较一下就行了

　　方案就构造一下就行了

092F(图论)

题意：

　　n个点m条边的有向图。对于每条边都要回答询问，询问内容是“如果把这条边反转，那么图中的强连通分量的个数是否会改变”。

　　n<=1000,m<=100000

分析：

　　首先不妨对原图求一下强连通分量，对于每条边(u,v)有两种情况

　　1、u和v在一个强连通分量中，那么这等价于判断如果删去边(u,v)，u是否还能通过其它路径走到v

　　2、u和v不在一个强连通分量中，那么这等价于判断如果删去边(u,v)，u是否还能通过其它路径走到v（如果可以，那么v->u，就形成了强连通分量）

　　所以问题的关键就是对于每条边如何快速判断如果删除这条边，那么还能否从u->v

　　如果暴力去做的话，那么是O(m(n+m))是会TLE的

　　我们考虑枚举每个点u去做一次dfs，在dfs过程中找出u的所有出边的答案

　　对于u的所有出边所对应的点，我们按顺序标成v1,v2,...,vk

　　我们按顺序从v1,v2,...,vk开始dfs，给尚未标号的节点进行标号，标号的内容是从哪个出边开始的

　　我们再按顺序从vk,...,v3,v2,v1开始dfs，给尚未标号的节点进行标号，标号的内容是从哪个出边开始的

　　那么v1,v2,...,vk都有两个标号了，分别是minlabel和maxlabel，如果某个vi的minlabel=maxlabel=i，那么从u->vi就只有这一条路能走

　　做一次dfs的时间复杂度是O(n+m)的，总的时间复杂度是O(n(n+m))