B. Mr. Kitayuta's Colorful Graph，二维并查集，一个简单变形就可以水过了~~

B. Mr. Kitayuta's Colorful Graph

->  Link 
<-

题目链接在上面，题目比较长，就不贴出来了，不过这是道很好的题，很多方法都可以做，真心邀请去A了这道题；

题意：n个顶点m条边的无向图，每输入的两个点之间可能有多种颜色连接在一起，然后查询时每输入两个点，问这两个点之间有多少条连接方式；

如图：

 
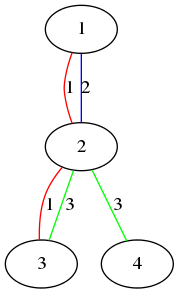
    1代表红色，2代表蓝色，3代表绿色；

这样3和4之间就是用绿色连接在一起的，他们之间只有一种连接方式，而2和3之间就有两种连接方式了，1和3只有一种（通过红色连接）；

题目就是求两个点之间有多少种连接方式；

思路： 一个并查集的变形，当时做的时候想，这不是一个单纯的并查集，通过不同的颜色判断是否联通；那我们怎么来处理这多种颜色呢，当时想了想并查集f[x]的含义，然后作了一个大胆的尝试，开一个二维并查集，既然f[x]储存的是x的父亲节点，那么我们用f[][],第一维表示颜色，第二维便是节点x,我们就用f[c][x]表示与颜色都为c的x的父亲节点，这样，在输入的时候，直接将颜色相同的两个点用并查集联通起来，然后查询的时候，因为颜色总共才100种，我们也可以在输入的时候将颜色最大值记录下来，然后从1开始遍历，如果两个节点都有与这种颜色的边相连，再用并查集进行判断是否联通，是，则有一种联通方式；如果不明白请看代码+注释：

const int N=100+10;
int v[N][N],f[N][N];
int find(int c,int x)
{
    return f[c][x]==-1?x:f[c][x]=find(c,f[c][x]);//第一维代表颜色，第二维代表节点；
}
int main()
{
   int n,m,q,i;
   while(~scanf("%d%d",&n,&m))
  {
      int uu,vv,c,cc=1;
      memset(v,0,sizeof(v));
      memset(f,-1,sizeof(f));
      for(i=0;i<m;i++)
      {
          scanf("%d%d%d",&uu,&vv,&c);
          v[uu][c]=1;
          v[vv][c]=1;//标记与顶点uu、vv相连的颜色存在；
          cc=max(cc,c);//记录颜色最大值；
          int xx=find(c,uu);//既然uu、vv都与颜色c相连，那就求出颜色为c时顶点x的父亲节点，如不相同，则联通起来；
          int yy=find(c,vv);
          if(xx!=yy)
            f[c][xx]=yy;//联通；
      }
      scanf("%d",&q);
      while(q--)
      {
          int sum=0;
          scanf("%d%d",&uu,&vv);
          for(i=1;i<=cc;i++)
            if(v[uu][i]&&v[vv][i])//颜色i与uu、vv都相连时判断其父亲节点是否相同，是，则联通；
            {
                int xx=find(i,uu);
                int yy=find(i,vv);
                if(xx==yy)
                    sum++;
            }
            printf("%d\n",sum);
      }
  }
    return 0;
}

考的还是对知识点的掌握程度，是否能灵活运用，博主也是碰巧想到了，真的要很大胆尝试，猜想，也就是稍加修改，一A而过~~