OpenCascade Eigenvalues and Eigenvectors of Square Matrix

OpenCascade Eigenvalues and Eigenvectors of Square Matrix

eryar@163.com

Abstract. OpenCascade use the Jacobi method to find the eigenvalues and the eigenvectors of a real symmetric square matrix. Use class math_Jacobi to computes all eigenvalues and eigenvectors by using Jacobi method. The exception NotSquare is raised if the matrix is not square. No verification that the matrix is really symmetric is done.

Key words. Eigenvalues, Eigenvectors, OpenCascade, Matrix, Jacobi method,

1. Introduction

工程技术中的一些问题，如振动问题和稳定性问题，常可归结为求一个方阵的特征值和特征向量的问题。数学中诸如方阵的对角化及解常微分方程等问题，也都有要用到特征值的理论。

定义：设A是n阶矩阵，如果数λ和n维非零列向量x使关系式 Ax = λx成立，那么这样的数λ称为方阵A的特征值，非零向量x称为A对应于特征值λ的特征向量。

推论：若n阶矩阵A与对角阵

相似，则λ1,λ2,...,λn即是A的n个特征值。

定理：n阶矩阵A与对角阵相似（即A能对角化）的充分必要条件是A有n个线性无关的特征向量。

推论：如果n阶矩阵A的n个特征值互不相等，则A与对角阵相似。

当A的特征方程有重根时，就不一定有n个线性无关的的特征向量，从而不一定能对角化。一个n阶矩阵具备什么条件才能对角化呢？这是一个较复杂的问题。

定理：设A为n阶对称阵，则有正交阵P，使

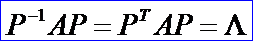
其中∧是以A的n个特征值为对角元的对角阵。

OpenCascacde中使用了Jacobi方法来计算对称方阵的特征值和特征向量。本文对math_Jacobi的使用进行详细说明。

2. Code Example

结合同济第四版《线性代数》中的例子，来验证Jacobi方法计算的结果。示例程序如下所示：

/*
*    Copyright (c) 2014 eryar All Rights Reserved.
*
*        File    : Main.cpp
*        Author  : eryar@163.com
*        Date    : 2014-06-22 21:46
*        Version : 1.0v
*
*    Description : Demonstrate how to find the eigenvalues and
*                  eigenvectors for a symmetric square Matrix.
*                  题目来自《线性代数》同济 第四版
*
*/

#define WNT

#include <math_Jacobi.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")

/**
* OpenCascade use Jacobi method to find the eigenvalues and
* the eigenvectors of a real symmetric square matrix.
*/
void EvalEigenvalue(const math_Matrix &A)
{
    math_Jacobi J(A);

    std::cout << A << std::endl;

    if (J.IsDone())
    {
        std::cout << "Jacobi: \n" << J << std::endl;
        //std::cout << "Eigenvalues: \n" << J.Values() << std::endl;
        //std::cout << "Eigenvectors: \n" << J.Vectors() << std::endl;

        for (Standard_Integer i = A.LowerRow(); i <= A.UpperRow(); ++i)
        {
            math_Vector V(, A.RowNumber());

            J.Vector(i, V);

            std::cout << "Eigenvalue: " << J.Value(i) << std::endl;
            std::cout << "Eigenvector: " << V << std::endl;
        }
    }
}

void TestJacobi(void)
{
    // 1. P120 Example 5:
    math_Matrix A1(, , , , 0.0);

    A1(, ) = 3.0;  A1(, ) = -1.0;
    A1(, ) = -1.0; A1(, ) = 3.0;

    EvalEigenvalue(A1);

    // 2. P120 Example 6:
    math_Matrix A2(, , , , 0.0);

    A2(, ) = -1.0; A2(, ) = 1.0; A2(, ) = 0.0;
    A2(, ) = -4.0; A2(, ) = 3.0; A2(, ) = 0.0;
    A2(, ) = 1.0;  A2(, ) = 0.0; A2(, ) = 2.0;

    EvalEigenvalue(A2);

    // 3. P120 Example 7:
    math_Matrix A3(, , , , 0.0);

    A3(, ) = -2.0; A3(, ) = 1.0; A3(, ) = 1.0;
    A3(, ) = 0.0;  A3(, ) = 2.0; A3(, ) = 0.0;
    A3(, ) = -4.0; A3(, ) = 1.0; A3(, ) = 3.0;

    EvalEigenvalue(A3);

    // 4. P127 Example 12:
    math_Matrix A4(, , , , 0.0);

    A4(, ) = 0.0;  A4(, ) = -1.0; A4(, ) = 1.0;
    A4(, ) = -1.0; A4(, ) = 0.0;  A4(, ) = 1.0;
    A4(, ) = 1.0;  A4(, ) = 1.0;  A4(, ) = 0.0;

    EvalEigenvalue(A4);

    // 5. P138 Execise 5(3);
    math_Matrix A5(, , , , 0.0);

    A5(, ) = 1.0; A5(, ) = 2.0; A5(, ) = 3.0;
    A5(, ) = 2.0; A5(, ) = 1.0; A5(, ) = 3.0;
    A5(, ) = 3.0; A5(, ) = 3.0; A5(, ) = 6.0;

    EvalEigenvalue(A5);
}

int main(int argc, char* argv[])
{
    // The Jacobi method to find the eigenvalues and
    // eigenvectors of a real symmetric square matrx.
    // The exception NotSquare is raised if the matrix is not square.
    // No verification that the matrix is really symmetric is done.
    TestJacobi();

    return ;
}

计算结果部分如下图所示：

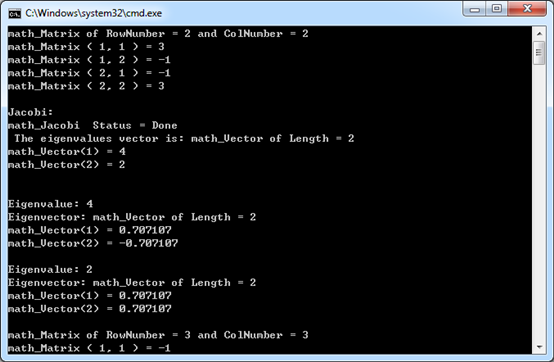
Figure 2.1 Jacobi method Result

3. Conclusion

矩阵的特征值和特征向量的理论能用来求解微分方程组的问题。振动分析、现代控制理论中的数学模型都可归结为对微分方程组的求解。因此，对特征值和特征向量的数值计算有重要的意义。

OpenCascade中提供了使用Jacobi方法来计算特征值和特征向量的类math_Jacobi。从计算结果可以看出，math_Jacobi只对对称方阵的计算结果准确，若不是对称阵，则计算结果是不准确的。

会使用OpenCascade中现成的算法是一回事，能实现这些算法又是另外一回事。对计算特征值和特征向量的数值方法感兴趣的读者，可以参考《计算方法》或《数值分析》等相关书籍。

4. References

1. 同济大学应用数学系. 线性代数. 高等教育出版社. 2003

2. 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002

3. 杨明, 李先忠. 矩阵论. 华中科技大学出版社. 2005

PDF Version: Eigenvalues and Eigenvectors of Square Matrix