连续小波变换（CWT）

整理下时频分析变换的方法，遇见好的文章就记录下来了，本篇博客参考知乎https://www.zhihu.com/topic/19621077/top-answers上的一个回答，自己手敲一遍，增强记忆

首先说明这里是连续小波变换，不会涉及离散小波变换，不涉及尺度函数。

对于一个morlet小波变换，其频率成分分别是4、6、10，具体表达式如下：

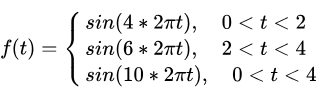
经小波变换，得到如下时频图：

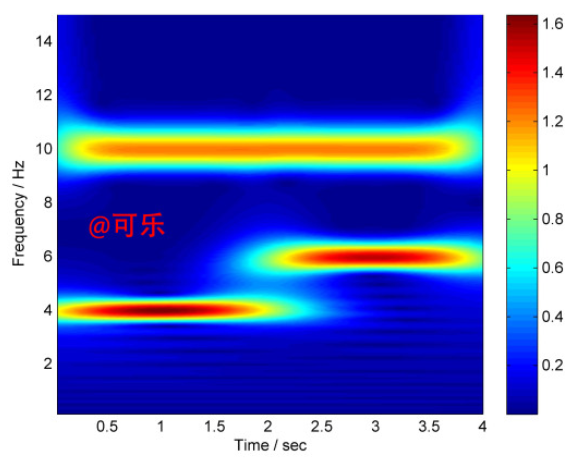
图一、二维时频图

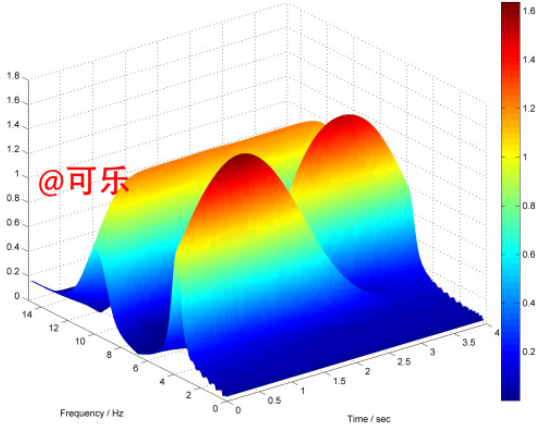
三维时频图

从图中可以清晰辨认出原始信号含有的频率成分及其个自对应的时间区间。如果你和我一样认真的话，你会产生三个疑问？

（1）为什么小波变换能确定信号频率和其对应的时间区间？
（2）为什么频率小的条纹比频率高的条纹要细？

（3）为什么三个条纹颜色的深浅不一样 ？

其实第（1）个问题可以从上一篇的博客中总结出来。

第一个问题我们把它一分为二，为什么CWT能辨认出信号的频率成分？为什么CWT能确定频率对应的时间区间？

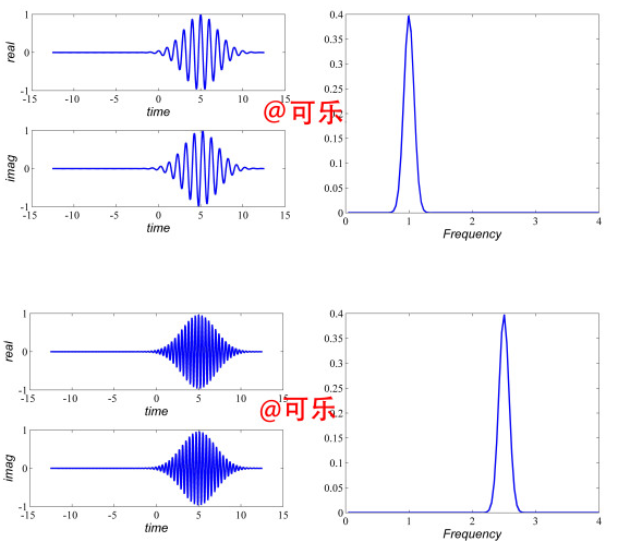
当然先看下公式。来一个morlet小波基函数表达式

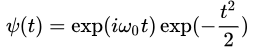
morlet小波的基函数是由复三角函数乘上一个指数衰减函数构成，这里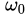表示中心频率。还是先看图（分别令）

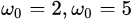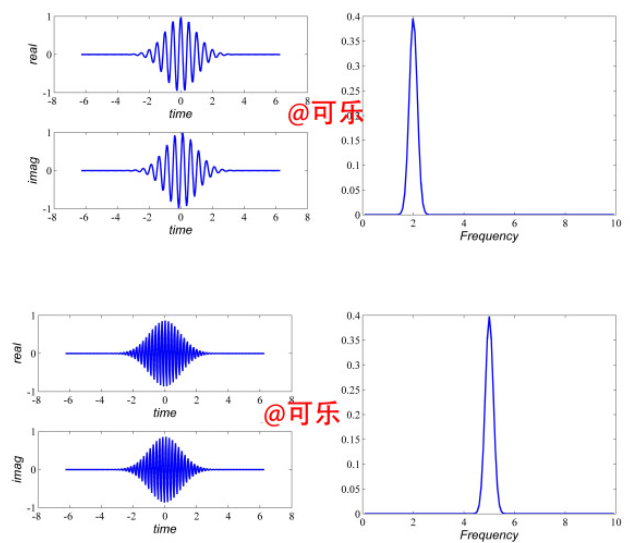
图三

上图左边是基函数时域图像，右边是傅里叶变换图像。可以看到基函数的频率正是其中心频率的值。这里给出morlet小波的傅里叶变换表达式

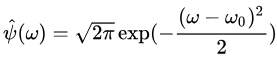
从表达式也可以看出当频率等于其中心频率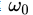时，取极大值。这里复三角函数可以辨认频率，衰减函数可以保证其时域的有限支撑。只给一个固定的中心频率可不能辨认信号的频率，同样，基函数只在【-2，2】之间也确定不了时间区间。所以这里的小波基函数需要平移和伸缩 。又是一个公式（按传统，这个变大时前还有一个根号a，但我不讨论这个）

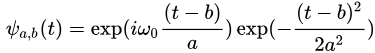
继续上图，给出b=5（平移因子）,a=2（尺度变量）,即平移5个单位，缩小2倍的morlet小波基函数的图像

图四

相对图三，从时域可以明显看出平移，从频域也很明显看出尺度伸缩。当然从傅里叶变换的性质也可以推断出来。

好了，基函数算是告一段落，下面是激动人心的时刻，还是得有公式。

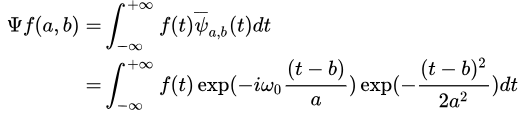
这算是morlet小波变换的公式了。

好，回到第一个问题，为什么小波变换能确定信号频率和其对应时间区域？

从时频图一可以看到，能看出条纹的部分明显是关于频率的积分极大值。

所以，把问题转换一下，为什么小波变换会在原始信号固有的频率上产生极大值，

而这极大值对应的区间正好是该频率的时区。连续小波变换的运算是什么？

是积分，是原始信号与小波基函数乘积后积分的过程，而积分就是一个求和的过程

举个例子：

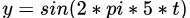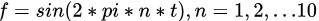一个频率为5的正弦函数，和乘积后积分，问当频率为何值时，他们的乘积积分后结果最大。答案你肯定知道，当两个正弦函数频率相等的时候，而就是n=5的时候，他们的乘积积分后最大。有图为证：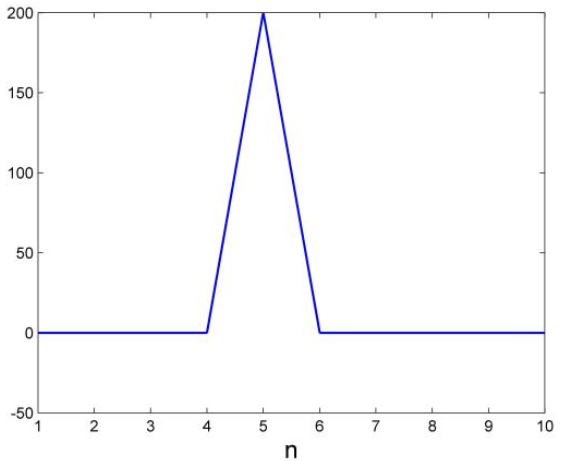

好，到这里你应该就明白了为什么小波变换会在原始信号固有的频率上产生极大值。因为基函数里包含复三角函数。

下面把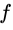换成小波基函数，换成morlet小波函数，去掉平移参数，并令初始中心频率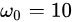，令尺度参数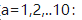

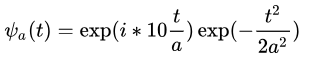
再次求其与y乘积积分后的最大值（这个得取模）。很明显，当a=2的时候，也就是小波基函数频率为5的时候，会取的极大值，如图

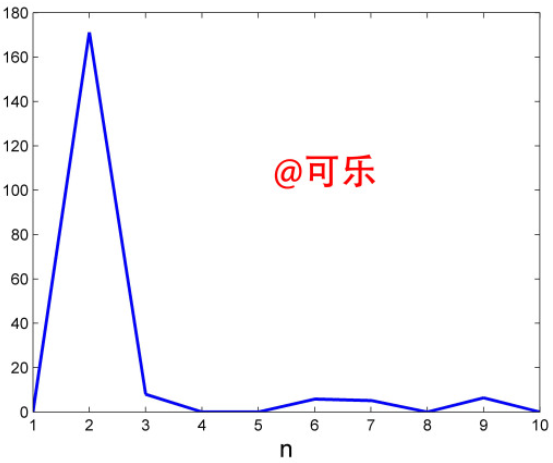
到这里，应该就很明朗了。小波小波，顾名思义，既要小又要有波动。morlet小波的波动性可以用复三角函数表达，小则用衰减函数表达，数学上把这种小称为有限支撑。即morlet小波的有限支撑是通过一个指数衰减函数实现的。复三角函数使其能分析频率（和原始信号乘积积分求极大值），衰减函数使其可以定位时间，他们加起来，才使得morlet小波可以用来做时频分析。

CWT就是选一个中心频率然后通过尺度变换得到一大堆中心频率，又通过时移得到一系列不同区间的基函数，分别和原始信号的某一段（对应基函数的区间）乘积再积分，产生的极值对应的频率就是原始信号这一区间含有的频率。

你不想换个角度看看吗？

换个角度，我们来从频域看看，好吗？根据傅里叶变化的性质Parseval公式可知：

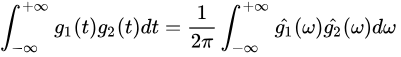
两信号乘积后时域的积分等于其 傅里叶变换后频率的积分。好，换成信号和小波基函数

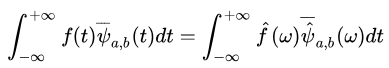
时域里面乘积积分看的不明显，频域里看就一目了然了，还是那个频率为5的原始信号，看看他的频域图像

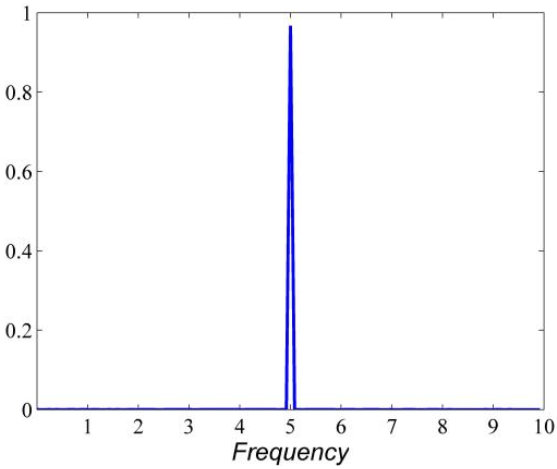
再看看五个中心频率不同的小波基函数

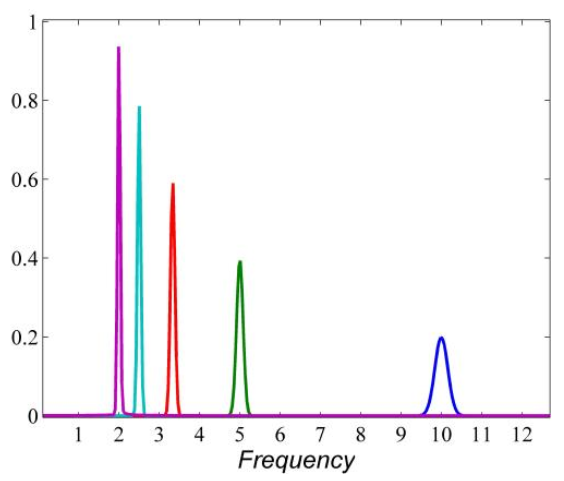
好了，两个函数再频域乘积再积分，又一次很明显，只有当小波中心频率为5的时候，小波基函数和原始信号乘积的积分才会取得极大值。其他的好像都是0啊

所以，小波可以认为是一个带通滤波器，只允许频率和小波中心频率（经过尺度伸缩后）相近的信号的通过