【剑指Offer】64、滑动窗口的最大值

  题目描述：

  给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

  解题思路：

  如果不考虑时间开销，使用蛮力法，本题并不难解决，依次遍历所有的滑动窗口，扫描每个窗口中的所有数字并找出其中的最大值，这都很容易实现，但是如果滑动窗口的大小为k，那么需要O(k)的时间找最大值，对于长度为n大的数组，总的时间复杂度为O(nk)。

  然后我们考虑进一步优化，一个滑动窗口实际上可以看成一个队列。当窗口滑动时，处于窗口第一个位置的数字被删除，同时在窗口的末尾又增加了一个新的数字。这符合队列“先进先出”的特性。

  在第20题：包含min函数的栈，我们使用两个栈实现了一个求最小值的栈，在O(1)时间内可以得到最小值，这里我们可以改为求最大值，同样可以在O(1)时间内得到最大值，而这里的数据用队列保存，我们可以用两个栈实现队列，这就是第5题：用两个栈实现队列。这样，实际上综合这两题我们可以解决本题，总的时间复杂度也可以降到O(n)。

  这里我们换用另外一种方法：使用双端队列。我们不把所有的值都加入滑动窗口，而是只把有可能成为最大值的数加入滑动窗口。这就需要一个两边都可以操作的双向队列。

  我们以数组{2,3,4,2,6,2,5,1}为例，滑动窗口大小为3，先把第一个数字2加入队列，第二个数字是3，比2大，所以2不可能是最大值，所以把2删除，3存入队列。第三个数是4，比3大，同样删3存4，此时滑动窗口以遍历三个数字，最大值4在队列的头部。

  第4个数字是2，比队列中的数字4小，当4滑出去以后，2还是有可能成为最大值的，因此将2加入队列尾部，此时最大值4仍在队列的头部。

  第五个数字是6，队列的数字4和2都比它小，所以删掉4和2，将6存入队列尾部，此时最大值6在队列头部。

  第六个数字是2，此时队列中的数6比2大，所以2以后还有可能是最大值，所以加入队列尾部，此时最大值6在仍然队列头部。

  ······

  依次进行，这样每次的最大值都在队列头部。

  还有一点需要注意的是：如果后面的数字都比前面的小，那么加入到队列中的数可能超过窗口大小，这时需要判断滑动窗口是否包含队头的这个元素，为了进行这个检查，我们可以在队列中存储数字在数组中的下标，而不是数值，当一个数字的下标和当前出来的数字下标之差大于等于滑动窗口的大小时，这个元素就应该从队列中删除。

  举例：

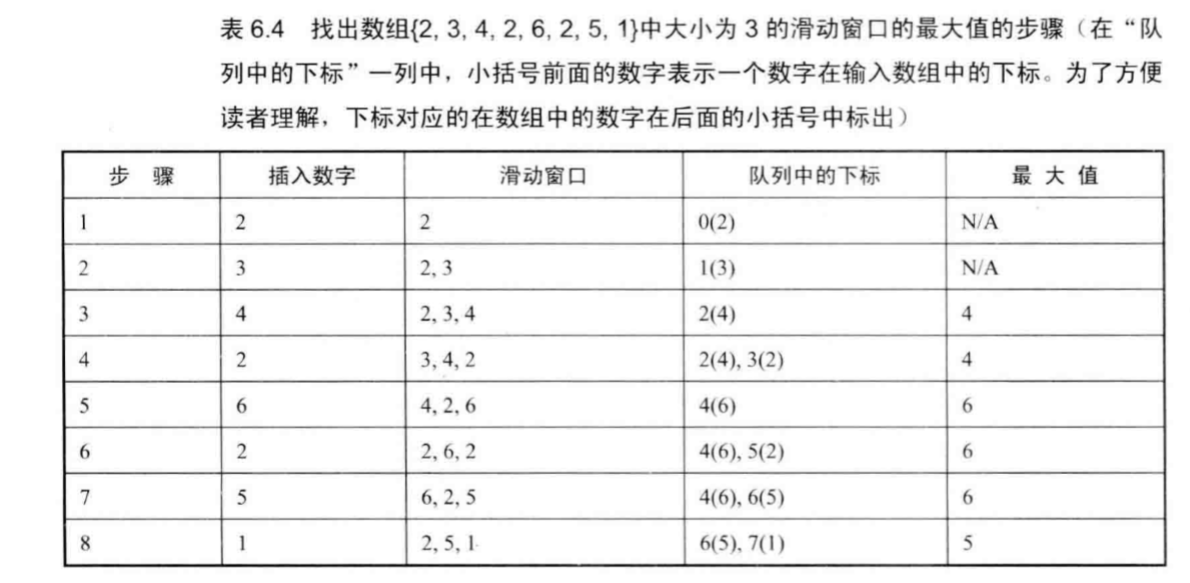
  编程实现（Java）：

import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size){
        /*
        思路：用双端队列实现
        */
        ArrayList<Integer> res=new ArrayList<>();
        if(num==null || num.length<1 || size<=0 || size>num.length)
            return res;
        Deque<Integer> queue=new LinkedList<>();
        for(int i=0;i<num.length;i++){
            while(!queue.isEmpty() && queue.peek()<i-size+1) //超出范围的去掉
                 queue.poll();
            //当前值大于之前的值，之前的不可能是最大值，可以删掉
            while(!queue.isEmpty() && num[i]>=num[queue.getLast()])
                 queue.removeLast();
            queue.add(i);
            if(i>=size-1){ //此时开始是第一个滑动窗口
                res.add(num[queue.peek()]);
            }
        }
        return res;
    }
}