BZOJ 3601: 一个人的数论

题目链接：www.lydsy.com/JudgeOnline/problem.php?id=3601

题意：

思路：

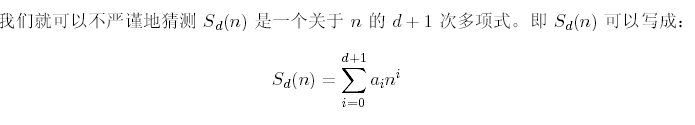
因此可以用高斯消元得到ai。

const int mod=1000000007;
const int N=111;

i64 myPow(i64 x,i64 y)
{
    if(y<0) return myPow(myPow(x,mod-2),-y);
    i64 ans=1;
    while(y)
    {
        if(y&1) ans=ans*x%mod;
        x=x*x%mod;
        y>>=1;
    }
    return ans;
}

i64 a[N][N],pp[N];
int n,p;

i64 A[N];

void init()
{
    int i,j;
    for(i=0;i<=p+1;i++)
    {
        pp[i]=myPow(i+1,p)+(i==0?0:pp[i-1]);
        pp[i]%=mod;
        a[i][p+2]=pp[i];
        a[i][0]=1;
        i64 pre=1;
        for(j=1;j<=p+1;j++)
        {
            pre=pre*(i+1)%mod;
            a[i][j]=pre;
        }
    }
    int k;
    for(i=0;i<=p+1;i++)
    {
        for(j=i;j<=p+1;j++) if(a[j][i]) break;
        if(i!=j)
        {
            for(k=0;k<=p+2;k++) swap(a[i][k],a[j][k]);
        }
        for(j=0;j<=p+1;j++) if(j!=i&&a[j][i])
        {
            i64 tmp=a[j][i]*myPow(a[i][i],-1)%mod;
            for(k=0;k<=p+2;k++) a[j][k]=(a[j][k]-tmp*a[i][k])%mod;
        }
    }
    for(i=0;i<=p+1;i++)
    {
        A[i]=a[i][p+2]*myPow(a[i][i],-1)%mod;
    }
}

int d[1111][2];

int main()
{

    scanf("%d%d",&p,&n);
    init();
    int i;

    for(i=1;i<=n;i++) scanf("%d%d",&d[i][0],&d[i][1]);
    i64 ans=0;
    for(i=0;i<=p+1;i++)
    {
        i64 tmp=1;
        int j;
        for(j=1;j<=n;j++)
        {
            tmp=tmp*myPow(d[j][0],(i64)d[j][1]*i)%mod;
            tmp=tmp*(1-myPow(d[j][0],p-i))%mod;
        }
        ans+=A[i]*tmp%mod;
    }
    ans%=mod;
    if(ans<0) ans+=mod;
    printf("%lld\n",ans);
}