poj 1704

Georgia and Bob

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7233		Accepted: 2173

Description

Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

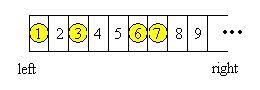
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win

Source

POJ Monthly--2004.07.18

 

转化成nim游戏，两个石子之间的间隔就是石子个数

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>

 using namespace std;

 const int MAX_N = ;
 int p[MAX_N];

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--) {
             int N;
             scanf("%d",&N);
             for(int i = ; i < N; ++i) {
                     scanf("%d",&p[i]);
             }
             if(N %  == ) p[N++] = ;
             sort(p, p + N);

             int x = ;
             for(int i = ; i +  < N; i += ) {
                     x ^= (p[i + ] - p[i] - );
             }

             if(x == ) printf("Bob will win\n");
             else printf("Georgia will win\n");
     }
     //cout << "Hello world!" << endl;
     return ;
 }