float浮点数的二进制存储方式及转换

int和float都是4字节32位表示形式。为什么float的范围大于int？

float精度为6～7位。1.66*10^10的数字结果并不是166 0000 0000 指数越大，误差越大。

这些问题，都是浮点数的存储方式造成的。

float和double在存储方式上都是遵从IEEE的规范的，float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。

无论是单精度还是双精度在存储中都分为三个部分：

1. 符号位(Sign) : 0代表正，1代表为负
2. 指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储
3. 尾数部分（Mantissa）：尾数部分

其中float的存储方式如下图所示：

而双精度的存储方式为:

   将一个float型转化为内存存储格式的步骤为：
     （）先将这个实数的绝对值化为二进制格式。
     （）将这个二进制格式实数的小数点左移或右移n位，直到小数点移动到第一个有效数字的右边。
     （）从小数点右边第一位开始数出二十三位数字放入第22到第0位。
     （）如果实数是正的，则在第31位放入“”，否则放入“”。
     （）如果n 是左移得到的，说明指数是正的，第30位放入“”。如果n是右移得到的或n=，则第30位放入“”。
     （）如果n是左移得到的，则将n减去1后化为二进制，并在左边加“”补足七位，放入第29到第23位。
         如果n是右移得到的或n=，则将n化为二进制后在左边加“”补足七位，再各位求反，再放入第29到第23位。

R32.24和R64.53的存储方式都是用科学计数法来存储数据的，比如8.25用十进制的科学计数法表示就为:8.25*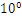,而120.5可以表示为:1.205*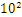,计算机根本不认识十进制的数据，他只认识0，1，所以在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示，8.25用二进制表示可表示为1000.01,120.5用二进制表示为：1110110.1用二进制的科学计数法表示1000.01可以表示为1.0001*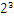,1110110.1可以表示为1.1101101*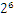,任何一个数都的科学计数法表示都为1.xxx*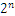,尾数部分就可以表示为xxxx,第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了，所以指数部分的存储采用移位存储，存储的数据为元数据+127，下面就看看8.25和120.5在内存中真正的存储方式。

首先看下8.25，用二进制的科学计数法表示为:1.0001*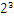

按照上面的存储方式，符号位为:0，表示为正，指数位为:3+127=130 ,位数部分为,故8.25的存储方式如下图所示:

而单精度浮点数120.5的存储方式如下图所示:

将一个内存存储的float二进制格式转化为十进制的步骤：
     （）将第22位到第0位的二进制数写出来，在最左边补一位“”，得到二十四位有效数字。将小数点点在最左边那个“”的右边。
     （）取出第29到第23位所表示的值n。当30位是“”时将n各位求反。当30位是“”时将n增1。
     （）将小数点左移n位（当30位是“”时）或右移n位（当30位是“”时），得到一个二进制表示的实数。
     （）将这个二进制实数化为十进制，并根据第31位是“”还是“”加上正号或负号即可。

那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据：0100001011101101000000000000，首先我们现将该数据分段，0 10000 0101 110 1101 0000 0000 0000 0000，在内存中的存储就为下图所示：

根据我们的计算方式，可以计算出，这样一组数据表示为:1.1101101*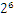=120.5

而双精度浮点数的存储和单精度的存储大同小异，不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了，只将120.5的最后存储方式图给出，大家可以仔细想想为何是这样子的

下面我就这个基础知识点来解决一个我们的一个疑惑，请看下面一段程序，注意观察输出结果

float f = 2.2f;
            double d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));
            f = 2.25f;
            d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));

可能输出的结果让大家疑惑不解，单精度的2.2转换为双精度后，精确到小数点后13位后变为了2.2000000476837，而单精度的2.25转换为双精度后，变为了2.2500000000000，为何2.2在转换后的数值更改了而2.25却没有更改呢？很奇怪吧？其实通过上面关于两种存储结果的介绍，我们已经大概能找到答案。首先我们看看2.25的单精度存储方式，很简单 0 1000 0001 001 0000 0000 0000 0000 0000,而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候，数值是不会变的，而我们再看看2.2呢，2.2用科学计数法表示应该为：将十进制的小数转换为二进制的小数的方法为将小数*2，取整数部分，所以0.282=0.4，所以二进制小数第一位为0.4的整数部分0，0.4×2=0.8，第二位为0,0.8*2=1.6,第三位为1，0.6×2 = 1.2，第四位为1，0.2*2=0.4，第五位为0，这样永远也不可能乘到=1.0，得到的二进制是一个无限循环的排列 00110011001100110011... ,对于单精度数据来说，尾数只能表示24bit的精度，所以2.2的float存储为:

但是这样存储方式，换算成十进制的值，却不会是2.2的，应为十进制在转换为二进制的时候可能会不准确，如2.2，而double类型的数据也存在同样的问题，所以在浮点数表示中会产生些许的误差，在单精度转换为双精度的时候，也会存在误差的问题，对于能够用二进制表示的十进制数据，如2.25，这个误差就会不存在，所以会出现上面比较奇怪的输出结果。

附注：

小数的二进制表示问题
       首先我们要搞清楚下面两个问题：
     ()  十进制整数如何转化为二进制数
           算法很简单。举个例子，11表示成二进制数：
                     /=   余
                       /=   余
                       /=   余
                       /=   余
                          0结束         11二进制表示为(从下往上):
          这里提一点：只要遇到除以后的结果为0了就结束了，大家想一想，所有的整数除以2是不是一定能够最终得到0。
          换句话说，所有的整数转变为二进制数的算法会不会无限循环下去呢？绝对不会，整数永远可以用二进制精确表示 ，但小数就不一定了。
      () 十进制小数如何转化为二进制数
           算法是乘以2直到没有了小数为止。举个例子，.9表示成二进制数
                     0.9*=1.8   取整数部分
                     0.8(.8的小数部分)*=1.6    取整数部分
                     0.6*=1.2   取整数部分
                     0.2*=0.4   取整数部分
                     0.4*=0.8   取整数部分
                     0.8*=1.6   取整数部分
                     0.6*=1.2   取整数部分
                              .........      .9二进制表示为(从上往下): ......
           注意：上面的计算过程循环了，也就是说*2永远不可能消灭小数部分，这样算法将无限下去。很显然，小数的二进制表示有时是不可能精确的 。
                其实道理很简单，十进制系统中能不能准确表示出1/3呢？同样二进制系统也无法准确表示1/。这也就解释了为什么浮点型减法出现了"减不尽"的精度丢失问题。