不失一般性和快捷性地判定决策单调（洛谷P1912 [NOI2009]诗人小G）（动态规划，决策单调性，单调队列）

闲话

如果哪年NOI（放心我这样的蒟蒻是去不了的）又来个决策单调性优化DP，那蒟蒻是不是会看都看不出来直接爆$0$？！

还是要想点办法，不失一般性也能快捷地判定决策单调。

对于判定决策单调的分析

再补一句决策单调性的概念：状态转移方程形如$f_i=\min/\max_{j=1}^{i-1} g_j+w_{i,j}$，且记$f_i$的最优决策点为$p_i$（也就是$f_i$从$g_{p_i}+w_{i,p_i}$处转移最优）若满足$p_i\le p_{i+1}$，则该方程满足决策单调性。（摘自蒟蒻的DP优化总结）

显然每个决策$j$可以用一个关于$i$的函数$f_j(i)$表示。

函数的一个重要思想：数形结合！

光靠脑子想不到规律，只好先举一些用语言难以描述的反例。我们的函数不能这样

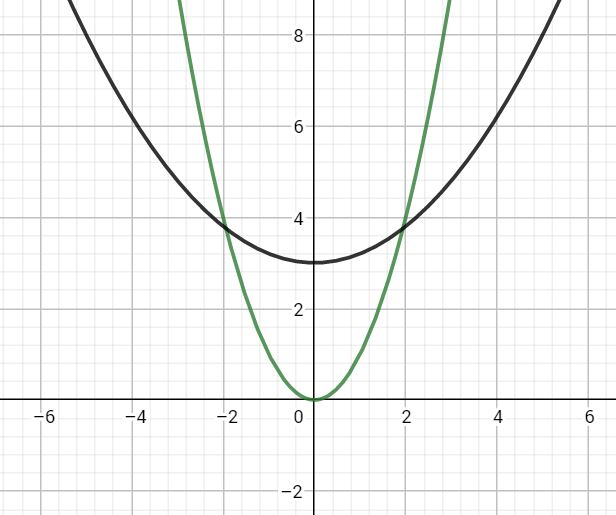
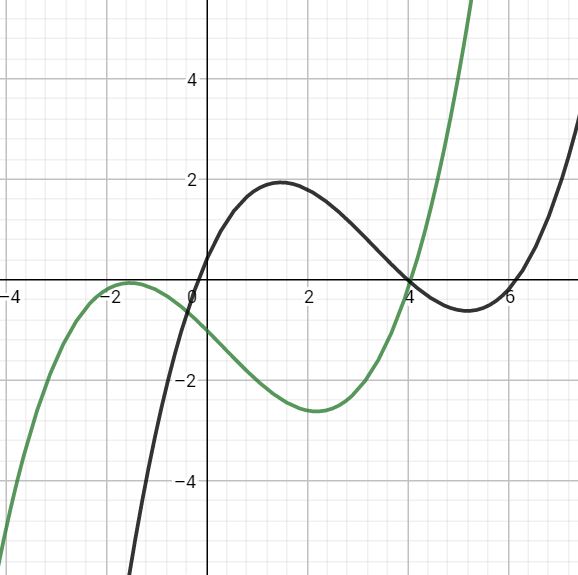
看到这里Dalao们有没有一点想法呢？蒟蒻反正想到了一点——两个函数必须只有一个交点！在这一点之前一个函数更优，而之后就被永远取代了。

感觉满足条件的函数其实很少，分类讨论一下（如有误欢迎Dalao指教）

直线

显然上面的基本要求都满足。不过要是函数是直线的话都可以用斜率优化搞了（$k_1x+b_1\ge k_2x+b_2,x\ge\frac{b_2-b_1}{k_1-k_2}$）。

不是直线

为了避免图1的尴尬情况，可能需要所有决策函数之间可以通过平移相互变换（形如$f_j(x)=f_k(x-a)+b$）。

为了避免图2的尴尬情况，可能需要函数的导函数在各自的定义域内单调递增/递减（注意是导函数不是原函数）。

接着，根据蒟蒻肝过的几个题，好像还有一条规律——

如果导函数递增、求最大值（柠檬），或者导函数递减、求最小值，要用单调栈。

如果导函数递增、求最小值（本题），或者导函数递减、求最大值（Lightning Conductor），要用单调队列。

复杂的函数

蒟蒻见过这一道（Yet another minimization problem）

感觉可以看成对于每一种数都有一个函数$\frac{(c_i-c_j)(c_i-c_j+1)}{2}$，单看这一个是满足决策单调性的（$c_i\ge c_j$，定义域内的导函数是递增的）。

那么总函数就可以写成$f_j(i)=g_j+\sum\frac{(c_i-c_j)(c_i-c_j+1)}{2}$，怎么看也不像是不满足决策单调性的。

本题的思路

那么就可以回归本题了。

设$len_i$为第$i$句的长度，$s_i=i+\sum\limits_{j=1}^i len_j$（加上$i$是默认一句话后面有空格）

设$f_i$为选前$i$句的最小代价，我们枚举当前这一行填入最后面的多少个句子，注意行末没有空格，长度要$-1$，那么有方程

\[f_i=\min\limits_{j=0}^{i-1}\{f_j+|s_i-s_j-1-L|^P\}
\]

容易发现后面这一坨决策函数是关于直线$x=s_j+1+L$对称的。把它去绝对值，变成两段，显然左边一段和右边一段的导函数都是递增的，左边恒$<0$，右边恒$>0$。又因为这函数是连续的，所以当然整个函数的导函数也单调递增咯！

用队列维护决策二分栈的过程不再赘述，总结里也有。时间复杂度$O(Tn\log n)$

看到Dalao们都记录了一个三元组，可蒟蒻还是觉得没啥必要啊。。。只要保存队列中相邻两个元素的临界值$k$就好了吧。

一个写法技巧：

二分决策$x,y(x<y)$的临界值的时候，左端点设成$x$就好了，没必要设成$1$（难怪蒟蒻之前写Lightning Conductor跑得有点慢）

三个坑点：

不管是转移还是输出，都要去掉行末的空格（怪蒟蒻看题不清）

当答案大于$10^{18}$的时候开longlong也炸了，所以要用实数以牺牲精度的代价换来更大的值域。然而double真的WA了。于是要开long double。

cmath的pow太慢了容易TLE，要手写快速幂。

#include<cstdio>

#include<cmath>

#include<cstring>

#define RG register

#define R RG int

#define G c=getchar()

#define Calc(i,j) f[j]+qpow(abs(s[i]-s[j]-L))//计算函数值

using namespace std;

typedef long double LD;//开long double

const int N=1e5+9;

int n,L,P,s[N],q[N],k[N],pr[N];

LD f[N];

char str[N][33];

inline int in(){

    RG char G;

    while(c<'-')G;

    R x=c&15;G;

    while(c>'-')x*=10,x+=c&15,G;

    return x;

}

inline LD qpow(RG LD b){//自己写快速幂

    RG LD a=1;

    for(R k=P;k;k>>=1,b*=b)

        if(k&1)a*=b;

    return a;

}

inline int bound(R x,R y){//二分临界值

    R l=x,r=n+1,m;//左端点设为x减小常数

    while(l<r){

        m=(l+r)>>1;

        Calc(m,x)>=Calc(m,y)?r=m:l=m+1;

    }

    return l;

}

int main(){

    R T=in(),i,h,t;

    while(T--){

        n=in();L=in()+1;P=in();//把L处理了一下

        for(i=1;i<=n;++i){

            if(scanf("%s",str[i]));

            s[i]=s[i-1]+strlen(str[i])+1;//记前缀和

        }

        for(q[i=h=t=1]=0;i<=n;++i){

            while(h<t&&k[h]<=i)++h;

            f[i]=Calc(i,q[h]);pr[i]=q[h];//记录转移位置方便输出方案

            while(h<t&&k[t-1]>=bound(q[t],i))--t;

            k[t]=bound(q[t],i);q[++t]=i;

        }

        if(f[n]>1e18)puts("Too hard to arrange");

        else{

            printf("%.0Lf\n",f[n]);

            for(q[t=0]=i=n;i;q[++t]=i=pr[i]);

            for(;t;--t){

                for(i=q[t]+1;i<q[t-1];++i)

                    printf("%s ",str[i]);

                puts(str[i]);//行末不要搞空格

            }

        }

        puts("--------------------");

    }

    return 0;

}