D6差分及树上差分

原谅我这篇博客拖了很久才写；

来到学校就和白痴一样缺了一世纪的课 上课特别懵；还有开学考枯了；

差分有列的差分，对于一段区间【l，r】进行修改，显然如果我们对于他的差分数组的l和r+1进行修改就可以了；

Xni=1a[i]

=(c[1]) + (c[1] + c[2]) + · · · + (c[1] + c[2] + · · · + c[n])

= n × c[1] + (n − 1) × c[2] + · · · + c[n]= n × (c[1] + c[2] + · · · + c[n])− (0 × c[1] + 1 × c[2] + · · · + (n − 1) × c[n])

所以，我们维护一个数组c2[i] = (i − 1) × c[i]在将区间[l,r] 的数全部+v 则还需同时将c2[l] + v × (i − 1), c2[r + 1] + (−v) × r 。

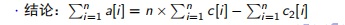
树上差分：分为点的差分和边的差分；

点的差分：

在一棵n个结点的树中，形容从si走到到ti的要求,求这条路径上的点被经过的次数。

显然，我们需要找到他们的LCA（中转点）。

我们需要让cnt[s] + +,让cnt[t] + +，而让他们的cnt[lca] − −，cnt[faher[lca]] − −;

最终统计即可；

边的差分不太一样；cnt[s] + +, cnt[t] + +, cnt[LCA]− =2；仔细画图理解一下；

第一题：BZOJ 4390

树上差分的模板题：

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e4+;
template<typename T>inline void read(T &x)
{
    x=;
    T f=,ch=getchar();
    while (!isdigit(ch)) ch=getchar();
    if (ch=='-') f=-, ch=getchar();
    while (isdigit(ch)) x=(x<<)+(x<<)+(ch^), ch=getchar();
    x*=f;
}
int ver[maxn<<],Next[maxn<<],head[maxn],len;
inline void add(int x,int y)
{
    ver[++len]=y,Next[len]=head[x],head[x]=len;
}
int fa[maxn],d[maxn],f[maxn][];
inline void dfs1(int x,int father,int deep)
{
    fa[x]=father,d[x]=deep;
    for (int i=;i<;++i)
        f[x][i]=f[f[x][i-]][i-];
    for (int i=head[x];i;i=Next[i])
    {
        int y=ver[i];
        if (y==father) continue;
        f[y][]=x;
        dfs1(y,x,deep+);
    }
}
inline int lca(int x,int y)
{
    if (d[x]>d[y]) swap(x,y);
    for (int i=;i>=;--i)
        if (d[f[y][i]]>=d[x])
            y=f[y][i];
    if (x==y) return x;
    for (int i=;i>=;--i)
        if (f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][];
}
int siz[maxn],sum[maxn],ans;
inline void dfs2(int x,int father)
{
    siz[x]=sum[x];
    for (int i=head[x];i;i=Next[i])
    {
        int y=ver[i];
        if (y==father) continue;
        dfs2(y,x);
        siz[x]+=siz[y];
    }
    ans=max(ans,siz[x]);
}
int main()
{
    int n,k;
    read(n);read(k);
    for (int i=;i<n;++i)
    {
        int x,y;
        read(x);read(y);
        add(x,y);add(y,x);
    }
    dfs1(,,);
    for (int i=;i<=k;++i)
    {
        int a,b;
        read(a);read(b);
        int c=lca(a,b);
        ++sum[a],++sum[b],--sum[c];
        if (c!=) --sum[fa[c]];
    }
    dfs2(,);
    printf("%d\n",ans);
    return ;
}

第二题：POJ 3417

题目大意：一棵有N个点的树，再往里面加入M条新边，现在要破坏其中的两条边，要求一条是原来树中的边，一条是新边，使其不连通。求方案的数量。

1 ≤ N ≤ 100000), 1 ≤ M ≤ 100000)

算法进阶好像也有；对于新加的一条边来说，肯定会与之前的树形成一个环，而此时环内的树上边和新加的这条边一同删除就会是一种方案。

而这道题是将所有新边都加入后的情况，那么我们看每条边，如果没有与它形成环的情况，那么这条边删除肯定会使得图不连通，即情况就会加M，也就是和新加的M条边任意组合都可以。

因而我们每次读入一条附加边，就给x到y的路径上的所有主要边记录上“被覆盖一次”，对于我们想要切割的一条主要边，有以下3种情况

1 若这条边被覆盖0次，则可以任意再切断一条附加边。
2 若这条边被覆盖1次，那么只能再切断唯一的一条附加边。
3 若这条边被覆盖2次及以上，没有可行的方案；

树上差分写一下；

#include<algorithm>
#include<bitset>
#include<cctype>
#include<cerrno>
#include<clocale>
#include<cmath>
#include<complex>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<limits>
#include<list>
#include<map>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<utility>
#include<vector>
#include<cwchar>
#include<cwctype>
using namespace std;
const int maxn=1e5+;
template<typename T>inline void read(T &x)
{
    x=;
    T f=,ch=getchar();
    while (!isdigit(ch)) ch=getchar();
    if (ch=='-') f=-, ch=getchar();
    while (isdigit(ch)) x=(x<<)+(x<<)+(ch^), ch=getchar();
    x*=f;
}
int ver[maxn<<],Next[maxn<<],head[maxn],len;
inline void add(int x,int y)
{
    ver[++len]=y,Next[len]=head[x],head[x]=len;
}
int fa[maxn],d[maxn],f[maxn][];
inline void dfs1(int x,int father,int deep)
{
    fa[x]=father,d[x]=deep;
    for (int i=;i<=;++i)
        f[x][i]=f[f[x][i-]][i-];
    for (int i=head[x];i;i=Next[i])
    {
        int y=ver[i];
        if (y==father) continue;
        f[y][]=x;
        dfs1(y,x,deep+);
    }
}
inline int lca(int x,int y)
{
    if (d[x]>d[y]) swap(x,y);
    for (int i=;i>=;--i)
        if (d[f[y][i]]>=d[x])
            y=f[y][i];
    if (x==y) return x;
    for (int i=;i>=;--i)
        if (f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][];
}
int siz[maxn],sum[maxn],ans;
inline void dfs2(int x,int father)
{
    siz[x]=sum[x];
    for (int i=head[x];i;i=Next[i])
    {
        int y=ver[i];
        if (y==father) continue;
        dfs2(y,x);
        siz[x]+=siz[y];
    }
}
int main()
{
    int n,m;
    read(n);read(m);
    for (int i=;i<n;++i)
    {
        int x,y;
        read(x);read(y);
        add(x,y);add(y,x);
    }
    dfs1(,,);
    for (int i=;i<=m;++i)
    {
        int a,b;
        read(a);read(b);
        int c=lca(a,b);
        ++sum[a],++sum[b],sum[c]-=;
    }
    dfs2(,);
    for (int i=;i<=n;++i)
        if (!siz[i] && i!=) ans+=m;
        else if (siz[i]==) ++ans;
    printf("%d\n",ans);
    return ;
}

View ；

第三题：LUOGU CF 739B

CF 739B；

如果v可以控制u,那么从v到u的路上的所有结点都可以控制u，因为从v到u路上的dist(v, u)是递减的。

可以每次遍历一个点的时候，二分找出根节点到当前点i路径上点，找出dist(j, i)刚好大于a[i]的点，树上差分统计这条路径。

而后遍历当前点i的所有儿子结点k，cnt[i]+ = cnt[k]

这里我写了倍增；

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+;
template<typename T>inline void read(T &x)
{
    x=;
    register int f=;
    register char ch=getchar();
    while (!isdigit(ch)) { if (ch=='-') f=-; ch=getchar();}
    while (isdigit(ch)) x=(x<<)+(x<<)+(ch^), ch=getchar();
    x*=f;
}
template<typename T>inline void print(T x)
{
    if (x<) putchar('-'),x=-x;
    if (x>) print(x/);
    putchar(x%+);
}
int ver[maxn<<],edge[maxn<<],Next[maxn<<],head[maxn],len;
inline void add(int x,int y,int z)
{
    ver[++len]=y,edge[len]=z,Next[len]=head[x],head[x]=len;
}
ll d[maxn];//必须用long long，否则过不了，如果你想一直莫名WA的话，可以不管
int f[maxn][];
int a[maxn];
int ans[maxn];
inline void dfs(int x,int fa,int dist)
{
    d[x]=d[fa]+dist,f[x][]=fa;
    for (int i=;i<=;++i)
        f[x][i]=f[f[x][i-]][i-];
    for (int i=head[x];i;i=Next[i])
    {
        int y=ver[i],z=edge[i];
        if (y==fa) continue;
        dfs(y,x,z);
        register int val=a[y],k=,now=y;
        while (k&&now)
        {
            if (d[now]-d[f[now][k]]<=val)
            {
                val-=d[now]-d[f[now][k]];
                now=f[now][k];
                k<<=;
            }
            else k>>=;
        }
        if (d[now]-d[f[now][]]<=val)
            now=f[now][];
        --ans[f[now][]],++ans[f[y][]];
    }
    ans[fa]+=ans[x];
}
int main()
{
    int n,y,z;read(n);
    for (int i=;i<=n;++i)
        read(a[i]);
    for (int i=;i<=n;++i)
    {
        read(y);read(z);
        add(i,y,z);add(y,i,z);
    }
    dfs(,,);
    for (int i=;i<=n;++i)
        print(ans[i]),putchar(' ');
    return ;
}

借教室：luoguP1083

二分能满足的订单数。差分数组，对于二分的一个值，先差分到当前订单，扫描维护前缀和即为当前借的教室数与d作比较即可；

#include <algorithm>
#include <cctype>
#include <cmath>
#include <complex>
#include <cstdio>
#include <cstring>
#include <deque>
#include <functional>
#include <list>
#include <map>
#include <iomanip>
#include <iostream>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#define sys system("PAUSE")
using namespace std;
const int maxn = 1e6 + ;
typedef long long ull;
inline int read()
{
    int x=,f=;
    char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-;ch=getchar();}
    while(isdigit(ch)) {x=(x<<)+(x<<)+(ch^);ch=getchar();}
    return x*f;
}
int n, m,a[maxn],d[maxn],r[maxn],l[maxn],c[maxn],sum[maxn],begin,end;
inline bool check(int k)
{
    memset(c, , sizeof(c));
    for(int i=;i<=k;++i)
    {
        c[l[i]]+=d[i];
        c[r[i]+]-=d[i];
    }
    for(int i=;i<=n;++i)
    {
        sum[i]=sum[i-]+c[i];
        if(sum[i]>a[i]) return false;
    }
    return true;
}

int main()
{
    n=read(),m=read();
    for (int i=;i<=n;++i) a[i]=read();
    for (int i=;i<=m;++i)
        d[i]=read(),l[i]=read(),r[i]=read();
    begin=,end=m;
    if(check(m))
    {
        printf("0\n");
        return ;
    }
    while(begin<end)
    {
        int mid=(begin+end)>>;
        if(check(mid)) begin=mid+;
        else end=mid;
    }
    printf("%d\n%d\n",-,begin);
    return ;
}

好啦我要去学生物必修二的什么自由组合蒙圈题了，毕竟还有琵琶行等我背呢；