CentOS Linux release 7.3破解密码详解
CentOS Linux release 7.3破解密码详解
作者:尹正杰
版权声明:原创作品,谢绝转载!否则将追究法律责任。
公司最近接了一个项目,拿到客户现有的源代码,但是服务器用户密码并不知情,开发进步了操作系统,一看是CentOs7.2的发型版本,领导问我是否有解决方案,这个时候就只能破解密码了。中间经历一个小插曲,起初按照百度的方法破解密码时出现了粘键的情况,百度上的一些资料说:在"LANG=zh_cn.UTF-8"同行后面加上“init=/bin/sh”,按照其方式进去之后,发现我的操作系统出现了粘键的情况,这一点很坑。
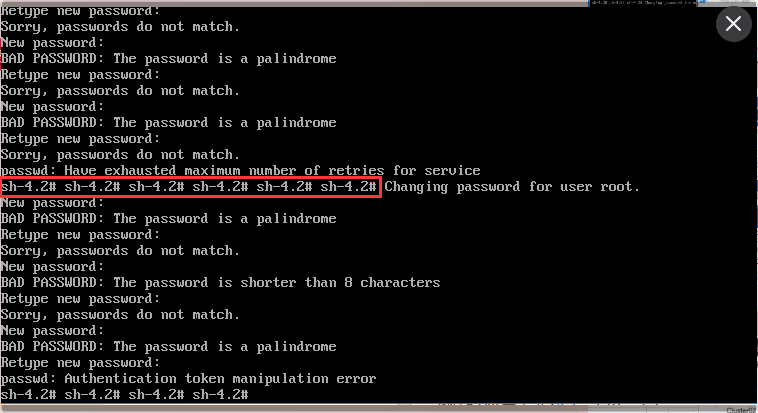
1.进入启动界面;
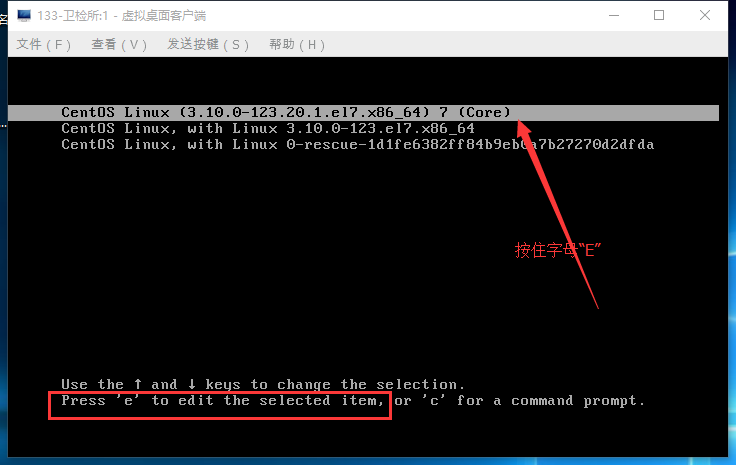
2.编辑启动文件;
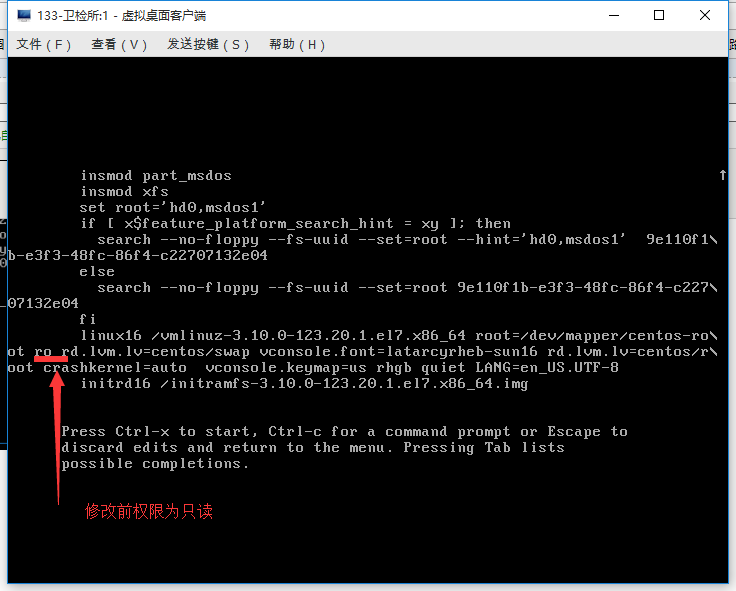
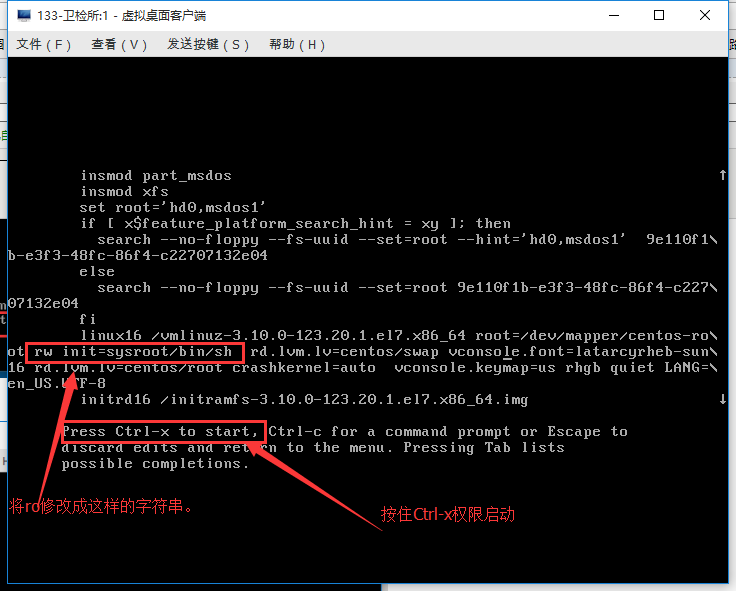
3.修改密码后进行重启.
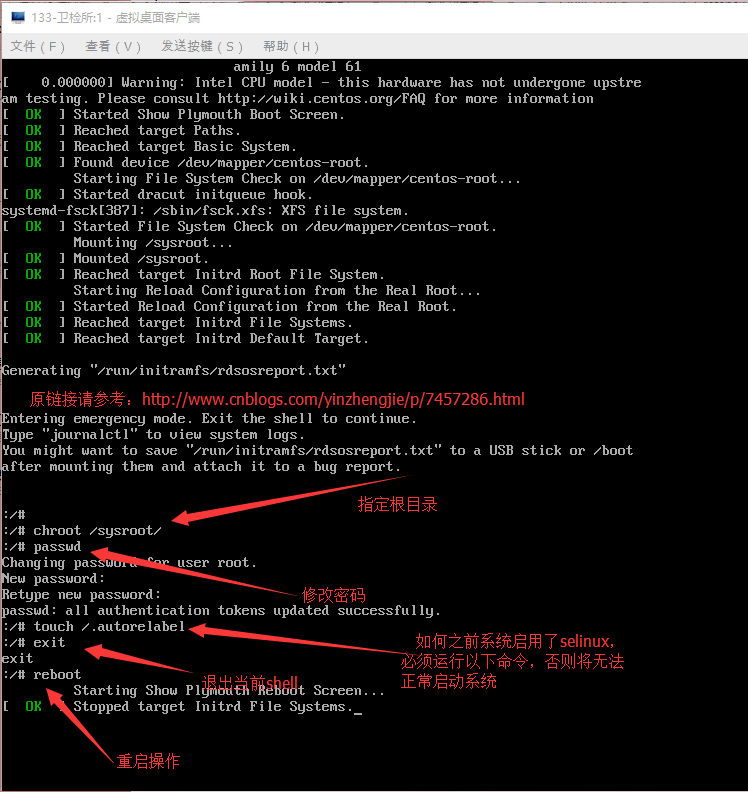
4.重启后登录操作系统即可

CentOS Linux release 7.3破解密码详解的更多相关文章
- CentOS \Linux 6版本系统命令及其使用详解
概述 常用的linux命令,分为文件管理.磁盘管理.用户管理.软件管理.系统管理等. 文件管理 ls命令 使用权限:所有使用者 使用方式:ls [-alrtAFR] [name...] 说明:显示指定 ...
- CentOS Linux release 7.3源码安装zabbix
CentOS Linux release 7.3安装zabbix 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 前言: 我去年用用centos6的环境搭建了一下 zabbix3.0 ...
- Linux/centos/redhat下各种压缩解压缩方式详解
1.zip命令 zip -r myfile.zip ./* 将当前目录下的所有文件和文件夹全部压缩成myfile.zip文件,-r表示递归压缩子目录下所有文件. 2.unzip unzip -o -d ...
- Centos Linux release 7.2.15ll (core) yum 安装java环境
系统版本 [root@localhost ~]# cat /etc/redhat-release CentOS Linux release 7.4.1708 (Core) #安装之前先查看一下有无系统 ...
- Linux中Nginx安装与配置详解
转载自:http://www.linuxidc.com/Linux/2016-08/134110.htm Linux中Nginx安装与配置详解(CentOS-6.5:nginx-1.5.0). 1 N ...
- (转)CentOS 6下配置软RAID图文详解
CentOS 6下配置软RAID图文详解 原文:http://blog.51cto.com/hujiangtao/1929620 一.RAID 简介 RAID 是英文Redundant Array o ...
- 【Linux学习】Linux下用户组、文件权限详解
原文地址:http://www.cnblogs.com/123-/p/4189072.html Linux下用户组.文件权限详解 用户组 在linux中的每个用户必须属于一个组,不能独立于组外.在li ...
- linux mount命令参数及用法详解
linux mount命令参数及用法详解 非原创,主要来自 http://www.360doc.com/content/13/0608/14/12600778_291501907.shtml. htt ...
- Oracle 11g客户端在Linux系统上的配置步骤详解
Oracle 11g客户端在Linux系统上的配置步骤详解 2011-07-26 10:47 newhappy2008 CSDN博客 字号:T | T 本文我们主要介绍了Oracle 11g客户端在L ...
随机推荐
- /var/lib/mysql 的访问权限问题 Can't connect to local MySQL server through socket '/var/lib/mysql/mysql.sock' (2)
mysql 登录不进去 提示Can't connect to local MySQL server through socket '/var/lib/mysql/mysql.sock' (2) she ...
- 第三个sprint冲刺第三阶段
公测版:
- spring mvc的工作原理
该文转载自:http://blog.csdn.net/u012191627/article/details/41943393 SpringMVC框架介绍 1) spring MVC属于SpringFr ...
- 常用的查询DOM的方法
查询body的方法=========== document.body // document.getElementsTagname("body")[0]; 查询html的方法=== ...
- 微信小程序开发3之保存数据及页面跳转
第一 保存本地数据 1.异步保存本地数据 wx.setStorage({ key:keyStr, data:dataStr, success: function(e){}, fail: functi ...
- BZOJ1087[SCOI2005]互不侵犯——状压DP
题目描述 在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案.国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子. 输入 只有一行,包含两个数N,K ( ...
- Educational Codeforces Round 23 B. Makes And The Product
B. Makes And The Product time limit per test 2 seconds memory limit per test 256 megabytes input sta ...
- FieldGroup绑定ItemDataSource
FieldGroup可以直接绑定一个数据源DataSource.但如果想绑定某个值,并没有直接作为数据库中的一个字段存在.而是最后转为json串保存在数据库中.这样的话相当于key-value模式的D ...
- Inside JVM 内存模型
Inside JVM 内存模型 来源 原文:https://blog.csdn.net/silentbalanceyh/article/details/4661230 参考:IBM开发中心文档,&l ...
- formelf.exe的用法
@2018-9-17 在windows下的cmd.exe程序下生成某个文件的 .txt版本 fromelf --text -o name.txt target.x
