一、关于聚类及相似度、距离的知识点

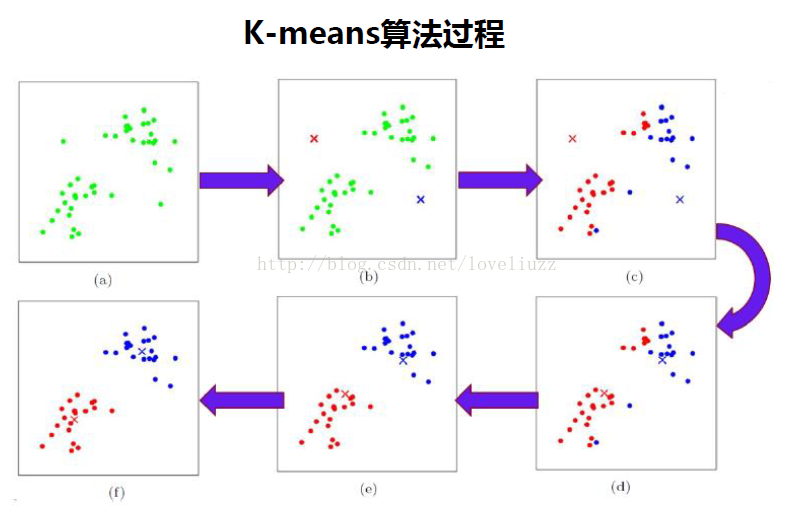
二、k-means算法思想与流程

三、sklearn中对于kmeans算法的参数

四、代码示例以及应用的知识点简介

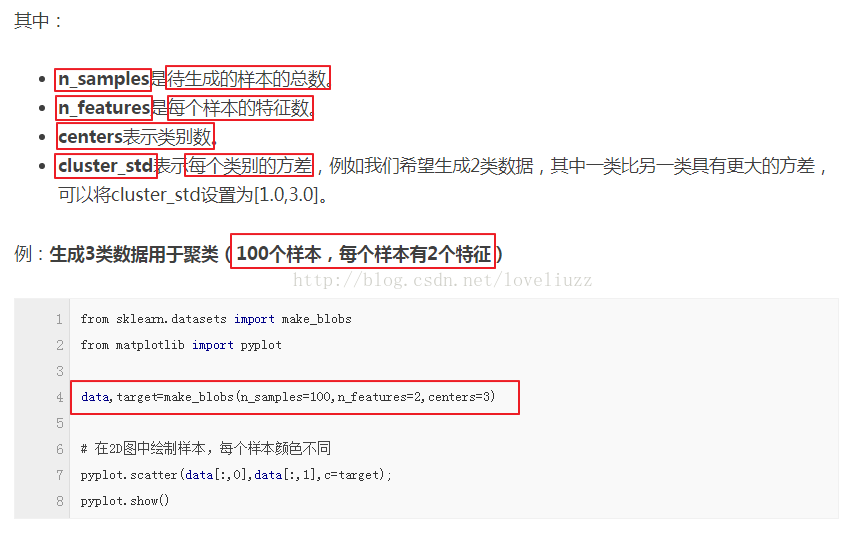
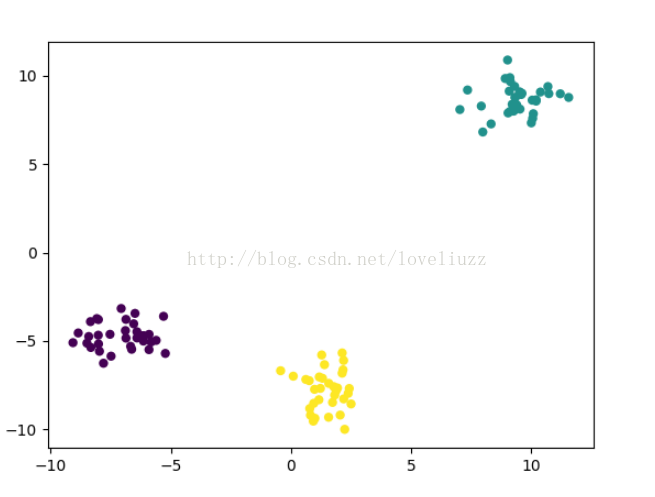
（1）make_blobs：聚类数据生成器

sklearn.datasets.make_blobs(n_samples=100, n_features=2,centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)[source]

返回值为：

（2）np.vstack方法作用——堆叠数组

详细介绍参照博客链接：http://blog.csdn.net/csdn15698845876/article/details/73380803

  1. #!/usr/bin/env python
  2. # -*- coding:utf-8 -*-
  3. # Author:ZhengzhengLiu
  4. #k-means聚类算法
  5. import numpy as np
  6. import pandas as pd
  7. import matplotlib as mpl
  8. import matplotlib.pyplot as plt
  9. import matplotlib.colors
  10. import sklearn.datasets as ds
  11. from sklearn.cluster import KMeans      #引入kmeans
  12. #解决中文显示问题
  13. mpl.rcParams['font.sans-serif'] = [u'SimHei']
  14. mpl.rcParams['axes.unicode_minus'] = False
  15. #产生模拟数据
  16. N = 1500
  17. centers = 4
  18. #make_blobs:聚类数据生成器
  19. data,y = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
  20. data2,y2 = ds.make_blobs(N,n_features=2,centers=centers,random_state=28)
  21. data3 = np.vstack((data[y==0][:200],data[y==1][:100],data[y==2][:10],data[y==3][:50]))
  22. y3 = np.array([0]*200+[1]*100+[2]*10+[3]*50)
  23. #模型的构建
  24. km = KMeans(n_clusters=centers,random_state=28)
  25. km.fit(data,y)
  26. y_hat = km.predict(data)
  27. print("所有样本距离聚簇中心点的总距离和:",km.inertia_)
  28. print("距离聚簇中心点的平均距离:",(km.inertia_/N))
  29. print("聚簇中心点:",km.cluster_centers_)
  30. y_hat2 = km.fit_predict(data2)
  31. y_hat3 = km.fit_predict(data3)
  32. def expandBorder(a, b):
  33. d = (b - a) * 0.1
  34. return a-d, b+d
  35. #画图
  36. cm = mpl.colors.ListedColormap(list("rgbmyc"))
  37. plt.figure(figsize=(15,9),facecolor="w")
  38. plt.subplot(241)
  39. plt.scatter(data[:,0],data[:,1],c=y,s=30,cmap=cm,edgecolors="none")
  40. x1_min,x2_min = np.min(data,axis=0)
  41. x1_max,x2_max = np.max(data,axis=0)
  42. x1_min,x1_max = expandBorder(x1_min,x1_max)
  43. x2_min,x2_max = expandBorder(x2_min,x2_max)
  44. plt.xlim((x1_min,x1_max))
  45. plt.ylim((x2_min,x2_max))
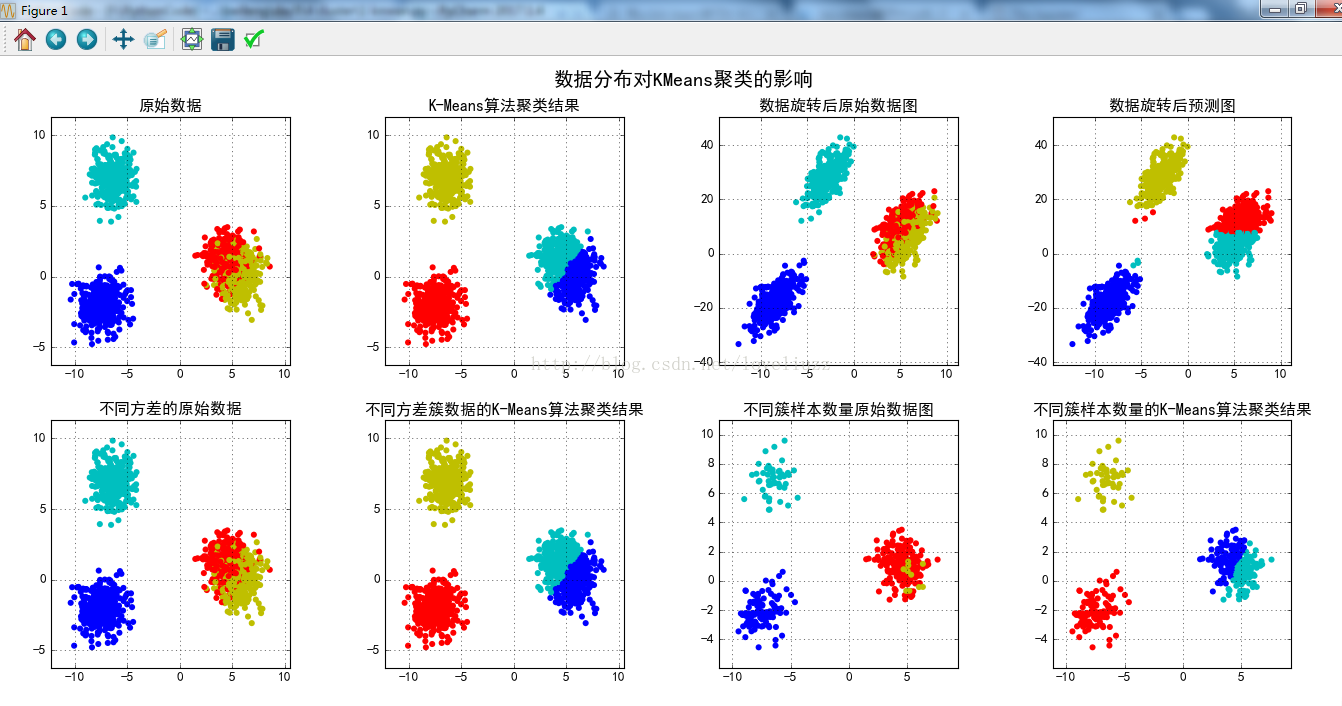
  46. plt.title("原始数据")
  47. plt.grid(True)
  48. plt.subplot(242)
  49. plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none')
  50. plt.xlim((x1_min, x1_max))
  51. plt.ylim((x2_min, x2_max))
  52. plt.title(u'K-Means算法聚类结果')
  53. plt.grid(True)
  54. m = np.array(((1, 1), (0.5, 5)))
  55. data_r = data.dot(m)
  56. y_r_hat = km.fit_predict(data_r)
  57. plt.subplot(243)
  58. plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
  59. x1_min, x2_min = np.min(data_r, axis=0)
  60. x1_max, x2_max = np.max(data_r, axis=0)
  61. x1_min, x1_max = expandBorder(x1_min, x1_max)
  62. x2_min, x2_max = expandBorder(x2_min, x2_max)
  63. plt.xlim((x1_min, x1_max))
  64. plt.ylim((x2_min, x2_max))
  65. plt.title(u'数据旋转后原始数据图')
  66. plt.grid(True)
  67. plt.subplot(244)
  68. plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
  69. plt.xlim((x1_min, x1_max))
  70. plt.ylim((x2_min, x2_max))
  71. plt.title(u'数据旋转后预测图')
  72. plt.grid(True)
  73. plt.subplot(245)
  74. plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
  75. x1_min, x2_min = np.min(data2, axis=0)
  76. x1_max, x2_max = np.max(data2, axis=0)
  77. x1_min, x1_max = expandBorder(x1_min, x1_max)
  78. x2_min, x2_max = expandBorder(x2_min, x2_max)
  79. plt.xlim((x1_min, x1_max))
  80. plt.ylim((x2_min, x2_max))
  81. plt.title(u'不同方差的原始数据')
  82. plt.grid(True)
  83. plt.subplot(246)
  84. plt.scatter(data2[:, 0], data2[:, 1], c=y_hat2, s=30, cmap=cm, edgecolors='none')
  85. plt.xlim((x1_min, x1_max))
  86. plt.ylim((x2_min, x2_max))
  87. plt.title(u'不同方差簇数据的K-Means算法聚类结果')
  88. plt.grid(True)
  89. plt.subplot(247)
  90. plt.scatter(data3[:, 0], data3[:, 1], c=y3, s=30, cmap=cm, edgecolors='none')
  91. x1_min, x2_min = np.min(data3, axis=0)
  92. x1_max, x2_max = np.max(data3, axis=0)
  93. x1_min, x1_max = expandBorder(x1_min, x1_max)
  94. x2_min, x2_max = expandBorder(x2_min, x2_max)
  95. plt.xlim((x1_min, x1_max))
  96. plt.ylim((x2_min, x2_max))
  97. plt.title(u'不同簇样本数量原始数据图')
  98. plt.grid(True)
  99. plt.subplot(248)
  100. plt.scatter(data3[:, 0], data3[:, 1], c=y_hat3, s=30, cmap=cm, edgecolors='none')
  101. plt.xlim((x1_min, x1_max))
  102. plt.ylim((x2_min, x2_max))
  103. plt.title(u'不同簇样本数量的K-Means算法聚类结果')
  104. plt.grid(True)
  105. plt.tight_layout(2, rect=(0, 0, 1, 0.97))
  106. plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18)
  107. plt.savefig("k-means聚类算法.png")
  108. plt.show()
  109. #运行结果：
  110. 所有样本距离聚簇中心点的总距离和: 2592.9990199
  111. 距离聚簇中心点的平均距离: 1.72866601327
  112. 聚簇中心点: [[ -7.44342199e+00  -2.00152176e+00]
  113. [  5.80338598e+00   2.75272962e-03]
  114. [ -6.36176159e+00   6.94997331e+00]
  115. [  4.34372837e+00   1.33977807e+00]]

代码中用到的知识点：

  1. #!/usr/bin/env python
  2. # -*- coding:utf-8 -*-
  3. # Author:ZhengzhengLiu
  4. #kmean与mini batch kmeans 算法的比较
  5. import time
  6. import numpy as np
  7. import matplotlib as mpl
  8. import matplotlib.pyplot as plt
  9. import matplotlib.colors
  10. from sklearn.cluster import KMeans,MiniBatchKMeans
  11. from sklearn.datasets.samples_generator import make_blobs
  12. from sklearn.metrics.pairwise import pairwise_distances_argmin
  13. #解决中文显示问题
  14. mpl.rcParams['font.sans-serif'] = [u'SimHei']
  15. mpl.rcParams['axes.unicode_minus'] = False
  16. #初始化三个中心
  17. centers = [[1,1],[-1,-1],[1,-1]]
  18. clusters = len(centers)     #聚类数目为3
  19. #产生3000组二维数据样本，三个中心点，标准差是0.7
  20. X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
  21. #构建kmeans算法
  22. k_means =  KMeans(init="k-means++",n_clusters=clusters,random_state=28)
  23. t0 = time.time()
  24. k_means.fit(X)      #模型训练
  25. km_batch = time.time()-t0       #使用kmeans训练数据消耗的时间
  26. print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
  27. #构建mini batch kmeans算法
  28. batch_size = 100        #采样集的大小
  29. mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
  30. t0 = time.time()
  31. mbk.fit(X)
  32. mbk_batch = time.time()-t0
  33. print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
  34. #预测结果
  35. km_y_hat = k_means.predict(X)
  36. mbk_y_hat = mbk.predict(X)
  37. #获取聚类中心点并对其排序
  38. k_means_cluster_center = k_means.cluster_centers_
  39. mbk_cluster_center = mbk.cluster_centers_
  40. print("K-Means算法聚类中心点:\n center=",k_means_cluster_center)
  41. print("Mini Batch K-Means算法聚类中心点:\n center=",mbk_cluster_center)
  42. order = pairwise_distances_argmin(k_means_cluster_center,mbk_cluster_center)
  43. #画图
  44. plt.figure(figsize=(12,6),facecolor="w")
  45. plt.subplots_adjust(left=0.05,right=0.95,bottom=0.05,top=0.9)
  46. cm = mpl.colors.ListedColormap(['#FFC2CC', '#C2FFCC', '#CCC2FF'])
  47. cm2 = mpl.colors.ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
  48. #子图1——原始数据
  49. plt.subplot(221)
  50. plt.scatter(X[:,0],X[:,1],c=Y,s=6,cmap=cm,edgecolors="none")
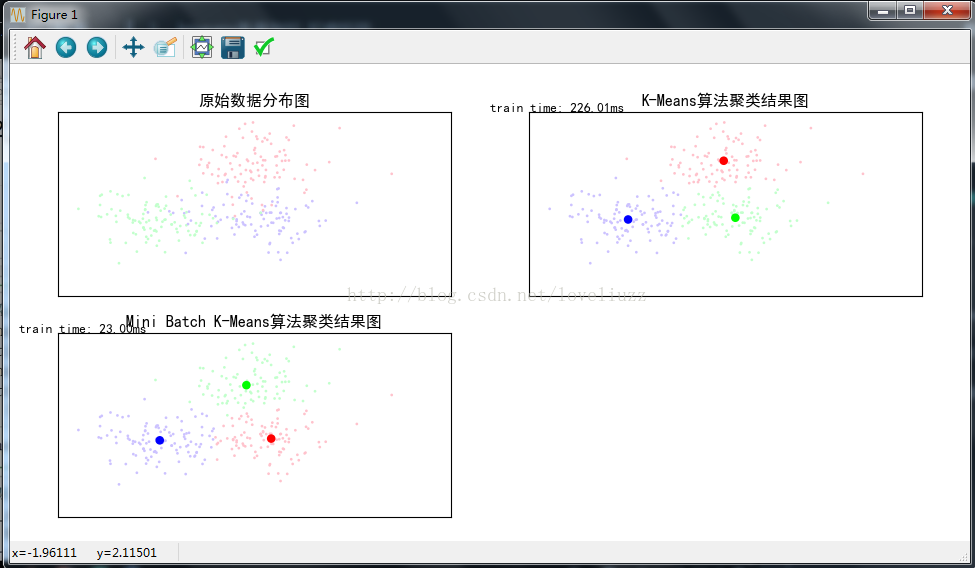
  51. plt.title(u"原始数据分布图")
  52. plt.xticks(())
  53. plt.yticks(())
  54. plt.grid(True)
  55. #子图2：K-Means算法聚类结果图
  56. plt.subplot(222)
  57. plt.scatter(X[:,0], X[:,1], c=km_y_hat, s=6, cmap=cm,edgecolors='none')
  58. plt.scatter(k_means_cluster_center[:,0], k_means_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
  59. plt.title(u'K-Means算法聚类结果图')
  60. plt.xticks(())
  61. plt.yticks(())
  62. plt.text(-3.8, 3,  'train time: %.2fms' % (km_batch*1000))
  63. plt.grid(True)
  64. #子图三Mini Batch K-Means算法聚类结果图
  65. plt.subplot(223)
  66. plt.scatter(X[:,0], X[:,1], c=mbk_y_hat, s=6, cmap=cm,edgecolors='none')
  67. plt.scatter(mbk_cluster_center[:,0], mbk_cluster_center[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
  68. plt.title(u'Mini Batch K-Means算法聚类结果图')
  69. plt.xticks(())
  70. plt.yticks(())
  71. plt.text(-3.8, 3,  'train time: %.2fms' % (mbk_batch*1000))
  72. plt.grid(True)
  73. plt.savefig("kmean与mini batch kmeans 算法的比较.png")
  74. plt.show()
  75. #运行结果：
  76. K-Means算法模型训练消耗时间:0.2260s
  77. Mini Batch K-Means算法模型训练消耗时间:0.0230s
  78. K-Means算法聚类中心点:
  79. center= [[ 0.96091862  1.13741775]
  80. [ 1.1979318  -1.02783007]
  81. [-0.98673669 -1.09398768]]
  82. Mini Batch K-Means算法聚类中心点:
  83. center= [[ 1.34304199 -1.01641075]
  84. [ 0.83760683  1.01229021]
  85. [-0.92702179 -1.08205992]]

五、聚类算法的衡量指标

    1. #!/usr/bin/env python
    2. # -*- coding:utf-8 -*-
    3. # Author:ZhengzhengLiu
    4. #聚类算法评估
    5. import time
    6. import numpy as np
    7. import matplotlib as mpl
    8. import matplotlib.pyplot as plt
    9. import matplotlib.colors
    10. from sklearn.cluster import KMeans,MiniBatchKMeans
    11. from sklearn import metrics
    12. from sklearn.metrics.pairwise import pairwise_distances_argmin
    13. from sklearn.datasets.samples_generator import make_blobs
    14. #解决中文显示问题
    15. mpl.rcParams['font.sans-serif'] = [u'SimHei']
    16. mpl.rcParams['axes.unicode_minus'] = False
    17. #初始化三个中心
    18. centers = [[1,1],[-1,-1],[1,-1]]
    19. clusters = len(centers)     #聚类数目为3
    20. #产生3000组二维数据样本，三个中心点，标准差是0.7
    21. X,Y = make_blobs(n_samples=300,centers=centers,cluster_std=0.7,random_state=28)
    22. #构建kmeans算法
    23. k_means =  KMeans(init="k-means++",n_clusters=clusters,random_state=28)
    24. t0 = time.time()
    25. k_means.fit(X)      #模型训练
    26. km_batch = time.time()-t0       #使用kmeans训练数据消耗的时间
    27. print("K-Means算法模型训练消耗时间:%.4fs"%km_batch)
    28. #构建mini batch kmeans算法
    29. batch_size = 100        #采样集的大小
    30. mbk = MiniBatchKMeans(init="k-means++",n_clusters=clusters,batch_size=batch_size,random_state=28)
    31. t0 = time.time()
    32. mbk.fit(X)
    33. mbk_batch = time.time()-t0
    34. print("Mini Batch K-Means算法模型训练消耗时间:%.4fs"%mbk_batch)
    35. km_y_hat = k_means.labels_
    36. mbkm_y_hat = mbk.labels_
    37. k_means_cluster_centers = k_means.cluster_centers_
    38. mbk_means_cluster_centers = mbk.cluster_centers_
    39. print ("K-Means算法聚类中心点:\ncenter=", k_means_cluster_centers)
    40. print ("Mini Batch K-Means算法聚类中心点:\ncenter=", mbk_means_cluster_centers)
    41. order = pairwise_distances_argmin(k_means_cluster_centers,
    42. mbk_means_cluster_centers)
    43. #效果评估
    44. ### 效果评估
    45. score_funcs = [
    46. metrics.adjusted_rand_score,    #ARI（调整兰德指数）
    47. metrics.v_measure_score,        #均一性与完整性的加权平均
    48. metrics.adjusted_mutual_info_score, #AMI（调整互信息）
    49. metrics.mutual_info_score,      #互信息
    50. ]
    51. ## 2. 迭代对每个评估函数进行评估操作
    52. for score_func in score_funcs:
    53. t0 = time.time()
    54. km_scores = score_func(Y, km_y_hat)
    55. print("K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs" % (score_func.__name__, km_scores, time.time() - t0))
    56. t0 = time.time()
    57. mbkm_scores = score_func(Y, mbkm_y_hat)
    58. print("Mini Batch K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs\n" % (score_func.__name__, mbkm_scores, time.time() - t0))
    59. #运行结果：
    60. K-Means算法模型训练消耗时间:0.6350s
    61. Mini Batch K-Means算法模型训练消耗时间:0.0900s
    62. K-Means算法聚类中心点:
    63. center= [[ 0.96091862  1.13741775]
    64. [ 1.1979318  -1.02783007]
    65. [-0.98673669 -1.09398768]]
    66. Mini Batch K-Means算法聚类中心点:
    67. center= [[ 1.34304199 -1.01641075]
    68. [ 0.83760683  1.01229021]
    69. [-0.92702179 -1.08205992]]
    70. K-Means算法:adjusted_rand_score评估函数计算结果值:0.72566；计算消耗时间:0.071s
    71. Mini Batch K-Means算法:adjusted_rand_score评估函数计算结果值:0.69544；计算消耗时间:0.001s
    72. K-Means算法:v_measure_score评估函数计算结果值:0.67529；计算消耗时间:0.004s
    73. Mini Batch K-Means算法:v_measure_score评估函数计算结果值:0.65055；计算消耗时间:0.004s
    74. K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.67263；计算消耗时间:0.006s
    75. Mini Batch K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.64731；计算消耗时间:0.005s
    76. K-Means算法:mutual_info_score评估函数计算结果值:0.74116；计算消耗时间:0.002s
    77. Mini Batch K-Means算法:mutual_info_score评估函数计算结果值:0.71351；计算消耗时间:0.001s

机器学习sklearn19.0聚类算法——Kmeans算法的更多相关文章

  1. [聚类算法] K-means 算法

    聚类 和 k-means简单概括. 聚类是一种 无监督学习 问题,它的目标就是基于 相似度 将相似的子集聚合在一起. k-means算法是聚类分析中使用最广泛的算法之一.它把n个对象根据它们的属性分为 ...

  2. 数据聚类算法-K-means算法

    深入浅出K-Means算法 摘要: 在数据挖掘中,K-Means算法是一种 cluster analysis 的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法. K-Mea ...

  3. 机器学习--聚类系列--K-means算法

    一.聚类 聚类分析是非监督学习的很重要的领域.所谓非监督学习,就是数据是没有类别标记的,算法要从对原始数据的探索中提取出一定的规律.而聚类分析就是试图将数据集中的样本划分为若干个不相交的子集,每个子集 ...

  4. 【转】 聚类算法-Kmeans算法的简单实现

    1. 聚类与分类的区别: 首先要来了解的一个概念就是聚类,简单地说就是把相似的东西分到一组,同 Classification (分类)不同,对于一个 classifier ,通常需要你告诉它“这个东西 ...

  5. 吴恩达机器学习笔记（七） —— K-means算法

    主要内容: 一.K-means算法简介 二.算法过程 三.随机初始化 四.二分K-means 四.K的选择 一.K-means算法简介 1.K-means算法是一种无监督学习算法.所谓无监督式学习,就 ...

  6. 数据挖掘经典算法——K-means算法

    算法描述 K-means算法是一种被广泛使用的基于划分的聚类算法,目的是将n个对象会分成k个簇.算法的具体描述如下: 随机选取k个对象作为簇中心: Do 计算所有对象到这k个簇中心的距离,将距离最近的 ...

  7. 算法 - k-means算法

    一.聚类思想 所谓聚类算法是指将一堆没有标签的数据自动划分成几类的方法,属于无监督学习方法,这个方法要保证同一类的数据有相似的特征,如下图所示:     根据样本之间的距离或者说是相似性(亲疏性),把 ...

  8. GMM算法k-means算法的比较

    1.EM算法 GMM算法是EM算法族的一个具体例子. EM算法解决的问题是:要对数据进行聚类,假定数据服从杂合的几个概率分布,分布的具体参数未知,涉及到的随机变量有两组,其中一组可观测另一组不可观测. ...

  9. 数据挖掘算法——K-means算法

    k-means中文称为K均值聚类算法,在1967年就被提出  所谓聚类就是将物理或者抽象对象的集合分组成为由类似的对象组成的多个簇的过程 聚类生成的组成为簇 簇内部任意两个对象之间具有较高的相似度,不 ...

随机推荐

  1. Java并发编程--总结

    1.并发优势 2.并发安全性 3.并发优化 4.并发内存模型 https://pan.baidu.com/s/1J4S2tC7YDgdOwtAg1970sg

  2. etcd raft如何实现leadership transfer

    leadership transfer可以把raft group中的leader身份转给其中一个follower.这个功能可以用来做负载均衡,比如可以把leader放在性能更好的机器或者离客户端更近的 ...

  3. apache 访问权限出错，apache selinux 权限问题， (13) Permission Denied

    今天在使用 httpd 做文件服务器的时候,发现 png 图像没有打开,但是原本www/html 文件夹内部的文件就可以打开.后来猜测是selinux 的问题,之前一直想写一篇关于selinux 的博 ...

  4. MongoDB的安装与python操作MongoDB

    一.安装MongoDB 因为我个人使用的是windows,就只记录下windows下的安装 1.下载安装 就是官网,下载msi,选个路径安装 2.配置 看见别的地方说需要手动在bin同级目录创建dat ...

  5. Java概述和项目演示

    Java概述和项目演示 1. 软件开发学习方法 多敲 多思考 解决问题 技术文档阅读(中文,英文) 项目文档 多阅读源码 2. 计算机 简称电脑,执行一系列指令的电子设备 3. 硬件组成 输入设备:键 ...

  6. windows7+apache2.4+sql server+php7.0

    参考文献:https://blog.csdn.net/blueheart20/article/details/76186218 https://blog.csdn.net/phpservice/art ...

  7. C# 动态方法和静态方法的区别

    C# 动态方法和静态方法的区别 (转) 动态方法与静态方法的区别: 1,使用方法上的区别:动态方法,在使用时需要先创建实例,才能调用实例方法,而静态方法则不需要,直接使用即可. 示例代码如下:静态方法 ...

  8. Alpha版本 - 展示博客

    Alpha版本 - 展示博客 S.W.S.D 成员简介 演示动态图 注册 登录 新建记录 分享记录 修改主页时间查看记录 文章模块 流星模块 修改用户信息(以头像为例) 用户使用概况 预期的典型用户 ...

  9. Java设计模式之四 ----- 适配器模式和桥接模式

    前言 在上一篇中我们学习了创建型模式的建造者模式和原型模式.本篇则来学习下结构型模式的适配器模式和桥接模式. 适配器模式 简介 适配器模式是作为两个不兼容的接口之间的桥梁.这种类型的设计模式属于结构型 ...

  10. synchronized关键字用法

    看到网上很多讲synchronized关键字用法的文章,说的都很有道理,也很深刻,但是看完总感觉脑袋里还是有点乱乱的.经过一番自己的思考后,想从自己的思考角度出发,来说一说synchronized关键 ...