树形DP 复习

树形DP

树形DP：建立在树上的动态规划

一般有两种传递方式：根→叶或叶→根

前者出现在换根DP中，一般操作是求出某一个点的最优解，再通过这一个点推知其他点的最优解。

后者是树形DP的常见形式，一般树形DP都是在叶子向根转移上。

一般状态都是f[x][...]表示x的子树中如何如何

POJ_3342_Party at Hali-Bula_树形DP

题目大意：没有上司的舞会，不存在选了连续两个点的情况，求最多选多少人。

题解：最裸的树形DP，直接状态，f[i][0]表示没选这个点，子树中最多选了多少个点。f[i][1]表示这个点选了，子树中最多选多少个点，之后每次max(f[son][0],f[son][1])更新f[x][0],之后f[son][0]更新f[x][1]

BZOJ_1864_[Zjoi2006]三色二叉树_树形DP

题目大意：

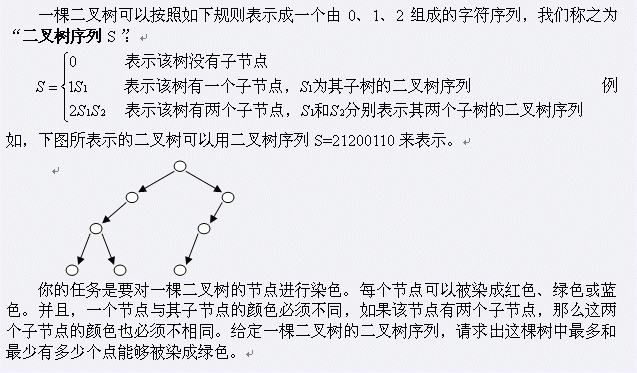
话说这道题的难点不在于树形DP啊...而是怎么把给你的东西转化成树啊...

树形DP很显然，f[x][1]表示这个点染成绿色的子树最大值，f[x]][0]表示没有染成绿色的子树最大值，（没有必要知道到底染成什么颜色，因为必定存在有解情况。）之后，直接转移一下。转移方程同上。

VIJOS P1144 小胖守皇宫

题目大意:
题意： 有一颗树， 每个节点是一个宫殿， 并且有个花费。 然后要驻扎人。 如果一个节点进驻了， 相邻的点，都会被监控。 问监控所有节点的最少花费。

相对于前两道题稍微复杂了一些。状态:f[x][0]表示x这个节点由儿子守的子树最小花费,f[x][1]表示这个点由自己守的子树最小花费,f[x][2]表示这个点由父亲守的子树最小花费。

之后转移就直接考虑一下那些状态全覆盖，那么就是f[x][1]可以从f[to][0,1,2]转移来，因为不论是哪一个，都满足要求，f[x][2]可以从f[to1][0,1]转移来，因为这两个也满足每一个节点都被守好了，而f[x][0]相对复杂一些，因为儿子节点只需要有一个守卫即可，那么我们考虑直接让f[x][0]从f[x][2]转移来，也就是在儿子节点中选择一个守卫与不守卫的差最小的一个。之后常规操作转移即可。

BZOJ_1060_时态同步_树形DP

题目大意：

给你一颗树，每次可以增加某一条路的长度，最后让所有根到叶子节点等长，求最小次数。

很显然，这是一个树形DP直接贪心的将所有子节点的距离改变成同一个，之后将子节点信息上传即可。

BZOJ_1040_[ZJOI2008]骑士_树形DP

题目大意：

给你一个基环树森林，之后选择若干个互相不直接相连的点，使权值最大。

树形DP比较显然，相对的来说就这是一类题型，基环树DP，找到每一个环，之后拆环分别DP最后合并答案即可。f[i][0]表示没选,f[i][1]表示选了，之后转移同上，每一个环有两种情况，找到环上任意一个边，断开，分别讨论两个都没选，选一个的情况，之后合并。

BZOJ_3037_创世纪_树形DP

题目大意：

给你n个点，每个点有一个父亲，求选择最大权值满足每个节点都有一个儿子不选。

同上，也是一个基环树DP，满足每个点都有一个入边，并且一共n个边，则必定为一个基环树。考虑状态，类似小胖守皇宫，但不太相同，f[x][0]表示这个点不选的子树最大权值和，f[x][1]表示这个点选的子树最大权值和，之后每次转移的时候找到一个儿子节点中f[x][0]-f[x][1]最大的，之后来更新f[x][1]，其他的直接贪心的要最大值即可，另外针对每个环，将其拆开分别讨论，作为子节点的分别讨论选与不选，而作为父节点的直接dfs一遍，求出对应的状态即可，最后答案+=max(f[son][1],f[son][0]),注意后者包含f[x][1]的情况。

BZOJ_1827_[Usaco2010 Mar]gather_奶牛大集会

题目大意：

给你一棵树，问以某一点为根的时候，所有点深度*点权的和最小

另一类树形DP，换根DP，一般这类题目都是给你一个树，之后问你所有点的信息，这个时候，暴力求是N^2的，但是可以以任意节点为根节点，之后求出根节点的值，之后再把信息从父节点→子节点转移求出对应答案即可。

这个题，先求出1为根的情况，之后每次传递给子节点。

BZOJ_1131_[POI2008]Sta

题目大意：

给你一颗树，之后问以某一个点为根的时候，所有点的深度和最小。

树形DP，直接转移，每次父亲节点，减去这个子节点的贡献，之后传递给子节点即可。