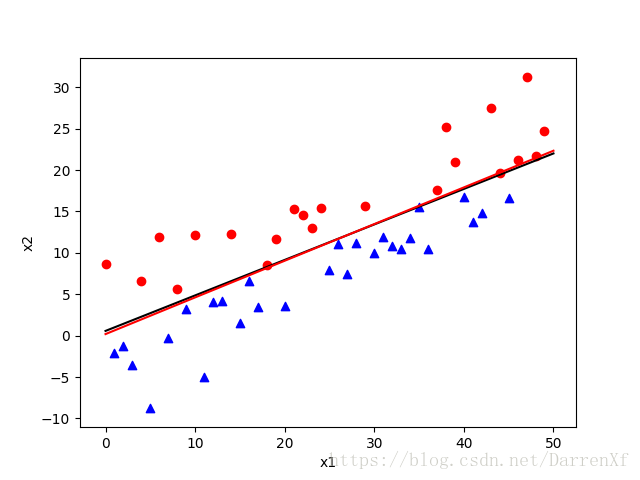
神经网络 感知机 Perceptron python实现

import numpy as np
import matplotlib.pyplot as plt
import math

def create_data(w1=3,w2=-7,b=4,seed=1,size=30):
    np.random.seed(seed)
    w = np.array([w1,w2])
    x1 = np.arange(0,size)
    v = np.random.normal(loc=0,scale=5,size=size)
    x2 = v - (b+w[0]*x1)/(w[1]*1.0)
    y_train=[]
    x_train = np.array(zip(x1,x2))
    for item in v:
        if item >=0:
            y_train.append(1)
        else:
            y_train.append(-1)
    y_train = np.array(y_train)
    return x_train,y_train

def SGD(x_train,y_train):
    alpha=0.01
    w,b=np.array([0,0]),0
    c,i=0,0
    while i<len(x_train):
        if (x_train[i].dot(w)+b)*y_train[i] <=0:
            c +=1
            w=w+alpha*y_train[i]*x_train[i]
            b=b+alpha*y_train[i]
            print("count:%s index:%s w:%s:b:%s" %(c,i,w,b))
            i=0
        else:
            i=i+1
    return w,b

def test_and_show(w1,w2,b,size,w_estimate,b_estimate,x_train,y_train):
    fig = plt.figure()
    ax1 = fig.add_subplot(111)
    plt.xlabel('x1')
    plt.ylabel('x2')
    x1 = np.arange(0,size+1,size)
    x2 = -(b+w1*x1)/(w2*1.0)
    ax1.plot(x1,x2,c="black")
    x2 = -(b_estimate+w_estimate[0]*x1)/w_estimate[1]*1.0
    ax1.plot(x1,x2,c="red")
    for i in range(0,len(x_train)):
        if y_train[i]>0:
            ax1.scatter(x_train[i,0],x_train[i,1],c="r",marker='o')
        else:
            ax1.scatter(x_train[i,0],x_train[i,1],c="b",marker="^")
    plt.show()

if __name__ == '__main__':
    w1,w2,b=3,-7,4
    size=50
    x_train,y_train=create_data(w1,w2,b,1,size)
    w_estimate,b_estimate=SGD(x_train,y_train)
    test_and_show(w1,w2,b,size,w_estimate,b_estimate,x_train,y_train)

count:1 index:0 w:[0.         0.08693155]:b:0.01
count:2 index:9 w:[-0.09        0.05511436]:b:0.0
count:3 index:8 w:[-0.01        0.11106631]:b:0.01
count:4 index:9 w:[-0.1         0.07924912]:b:0.0
count:5 index:8 w:[-0.02        0.13520107]:b:0.01
count:6 index:9 w:[-0.11        0.10338388]:b:0.0
count:7 index:8 w:[-0.03        0.15933583]:b:0.01
count:8 index:9 w:[-0.12        0.12751864]:b:0.0
count:9 index:8 w:[-0.04        0.18347059]:b:0.01
count:10 index:9 w:[-0.13       0.1516534]:b:0.0
count:11 index:8 w:[-0.05        0.20760535]:b:0.01
count:12 index:9 w:[-0.14        0.17578815]:b:0.0
count:13 index:8 w:[-0.06        0.23174011]:b:0.01
count:14 index:9 w:[-0.15        0.19992291]:b:0.0
count:15 index:8 w:[-0.07        0.25587487]:b:0.01
count:16 index:9 w:[-0.16        0.22405767]:b:0.0
count:17 index:8 w:[-0.08        0.28000963]:b:0.01
count:18 index:9 w:[-0.17        0.24819243]:b:0.0
count:19 index:18 w:[0.01       0.33316026]:b:0.01
count:20 index:7 w:[-0.06        0.33550632]:b:0.0
count:21 index:9 w:[-0.15        0.30368913]:b:-0.01
count:22 index:18 w:[0.03       0.38865696]:b:0.0
count:23 index:7 w:[-0.04        0.39100302]:b:-0.01
count:24 index:9 w:[-0.13        0.35918582]:b:-0.02
count:25 index:16 w:[-0.29        0.29352152]:b:-0.03
count:26 index:8 w:[-0.21        0.34947347]:b:-0.02
count:27 index:18 w:[-0.03       0.4344413]:b:-0.01
count:28 index:9 w:[-0.12        0.40262411]:b:-0.02
count:29 index:9 w:[-0.21        0.37080691]:b:-0.03
count:30 index:18 w:[-0.03        0.45577474]:b:-0.02
count:31 index:9 w:[-0.12        0.42395755]:b:-0.03
count:32 index:9 w:[-0.21        0.39214035]:b:-0.04
count:33 index:18 w:[-0.03        0.47710818]:b:-0.03
count:34 index:9 w:[-0.12        0.44529098]:b:-0.04
count:35 index:9 w:[-0.21        0.41347379]:b:-0.05
count:36 index:18 w:[-0.03        0.49844162]:b:-0.04
count:37 index:9 w:[-0.12        0.46662442]:b:-0.05
count:38 index:9 w:[-0.21        0.43480723]:b:-0.06
count:39 index:18 w:[-0.03        0.51977506]:b:-0.05
count:40 index:9 w:[-0.12        0.48795786]:b:-0.06
count:41 index:9 w:[-0.21        0.45614067]:b:-0.07
count:42 index:44 w:[0.23       0.65296677]:b:-0.06
count:43 index:7 w:[0.16       0.65531283]:b:-0.07
count:44 index:7 w:[0.09       0.65765889]:b:-0.08
count:45 index:7 w:[0.02       0.66000495]:b:-0.09
count:46 index:9 w:[-0.07        0.62818775]:b:-0.1
count:47 index:9 w:[-0.16        0.59637056]:b:-0.11
count:48 index:9 w:[-0.25        0.56455336]:b:-0.12
count:49 index:44 w:[0.19       0.76137946]:b:-0.11
count:50 index:7 w:[0.12       0.76372552]:b:-0.12
count:51 index:7 w:[0.05       0.76607158]:b:-0.13
count:52 index:7 w:[-0.02        0.76841764]:b:-0.14
count:53 index:9 w:[-0.11        0.73660045]:b:-0.15
count:54 index:9 w:[-0.2         0.70478325]:b:-0.16
count:55 index:9 w:[-0.29        0.67296605]:b:-0.17
count:56 index:35 w:[-0.64      0.517885]:b:-0.18
count:57 index:8 w:[-0.56        0.57383695]:b:-0.17
count:58 index:8 w:[-0.48        0.62978891]:b:-0.16
count:59 index:8 w:[-0.4         0.68574086]:b:-0.15
count:60 index:18 w:[-0.22        0.77070869]:b:-0.14
count:61 index:9 w:[-0.31       0.7388915]:b:-0.15
count:62 index:35 w:[-0.66        0.58381044]:b:-0.16
count:63 index:8 w:[-0.58       0.6397624]:b:-0.15
count:64 index:8 w:[-0.5         0.69571435]:b:-0.14
count:65 index:8 w:[-0.42        0.75166631]:b:-0.13
count:66 index:18 w:[-0.24        0.83663414]:b:-0.12
count:67 index:9 w:[-0.33        0.80481694]:b:-0.13
count:68 index:26 w:[-0.59       0.6938186]:b:-0.14
count:69 index:8 w:[-0.51        0.74977055]:b:-0.13
count:70 index:8 w:[-0.43       0.8057225]:b:-0.12
count:71 index:18 w:[-0.25        0.89069034]:b:-0.11
count:72 index:9 w:[-0.34        0.85887314]:b:-0.12
count:73 index:16 w:[-0.5         0.79320884]:b:-0.13
count:74 index:18 w:[-0.32        0.87817667]:b:-0.12
count:75 index:16 w:[-0.48        0.81251236]:b:-0.13
count:76 index:18 w:[-0.3         0.89748019]:b:-0.12
count:77 index:9 w:[-0.39      0.865663]:b:-0.13
count:78 index:44 w:[0.05      1.0624891]:b:-0.12
count:79 index:9 w:[-0.04       1.0306719]:b:-0.13
count:80 index:9 w:[-0.13        0.99885471]:b:-0.14
count:81 index:9 w:[-0.22        0.96703751]:b:-0.15
count:82 index:9 w:[-0.31        0.93522032]:b:-0.16
count:83 index:9 w:[-0.4         0.90340312]:b:-0.17