二叉树c++实现
!!版权声明:本文为博主原创文章,版权归原文作者和博客园共有,谢绝任何形式的 转载!!
作者:mohist
--- 欢迎指正---
二叉树特点:
要么为空树;要么,当前结点的左孩子比当前结点值小,当前结点的右孩子比当前结点的值大。
1、插入:
1.1 插入结点的值比当前结点的值小,继续找当前结点的左子树,
1.2 插入结点的值比当前结点的值大,继续找当前结点的右子树,
1.3 找到合适的位置了,插入树。
2、删除:
2.1 删除结点是叶子结点,直接将其删除即可
2.2 删除结点只有左孩子或者只有右孩子,将其孩子结点删除,并将指向孩子结点的分支设置为空,c++是设置为NULL。不过更好的做法是,将孩子结点的值替换到当前结点,再删除孩子结点即可。
2.3 删除的结点同时含有左孩子与右孩子,需要找到删除结点的后继结点,将后继结点作为当前结点。
完整源码:
#include <iostream>
using namespace std; struct node
{
// 数据域
int data; // 左节点
node *lc; // 右结点
node *rc; // 构造函数
node()
: data(0)
, lc(NULL)
, rc(NULL)
{
}
}; // bst
class bstree
{
public:
enum
{
hmax_size_32767 = 32767,
hmin_size_0 = 0,
}; public: // 构造函数
bstree()
: root(NULL)
, size(0)
{
} // 析构函数
virtual ~bstree(){} int get_size()
{
return size;
} // 插入结点
void insert_node(int data)
{
int cur_size = get_size();
if (hmax_size_32767 == cur_size)
{
cout << "insert node error, the size of the tree is max" << endl;
return ;
}
root = insert(root, data);
} // 先序遍历(前序遍历)
void pre_order()
{
pre_order_traverse(root);
} // 中序遍历
void in_order()
{
in_order_traverse(root);
} // 后序遍历
void post_order()
{
post_order_traverse(root);
} /*
查找某个结点
int key - 查找结果 返回值:
NULL : 可能为root为空 或者 没有找到
!= NULL, 找到结点
*/
node* query(int key)
{
if (NULL == root)
{
cout << "query error, root = null" << endl;
return NULL;
} return query_node(root, key);
} // 删除树
void remove_all()
{
if (NULL == root)
{
cout << "remove all failed, root = null" << endl;
return;
} remove_all(root); int cur_size = get_size();
if (0 == cur_size)
root = NULL;
} // 删除某个结点
void remove_node(int del_data)
{
if (NULL == root)
{
cout << "remove node error, root = null" << endl;
return;
} node *parent_node = NULL;
node *del_node = root; // 找到删除结点的父节点与删除结点
while (del_node)
{
if (del_data == del_node->data)
break;
else if (del_data > del_node->data)
{
parent_node = del_node;
del_node = del_node->rc;
}
else if (del_data < del_node->data)
{
parent_node = del_node;
del_node = del_node->lc;
}
} // 若没有找到要删除的结点
if (NULL == del_node)
{
cout << "remove node error, " << del_data << " was not find" << endl;
return;
} // 1、若删除的结点没有左子树和右子树
if ( (NULL == del_node->lc) && (NULL == del_node->rc) )
{
// 为什么要先判断根结点,因为根结点的父节点找不到,结果为NULL,
// 1.1 可能只有一个根结点, 将root释放值为空
if (del_node == root)
{
root = NULL;
delete del_node;
del_node = NULL; dec_size();
return;
} // 1.2 非根结点,那就是叶子结点了, 将父节点指向删除结点的分支指向NULL
if (del_node == parent_node->lc)
parent_node->lc = NULL;
else if (del_node == parent_node->rc)
parent_node->rc = NULL; // 释放结点
delete del_node;
del_node = NULL;
dec_size();
} // 2、若删除结点只有左孩子,没有右孩子
else if ( (NULL != del_node->lc) && (NULL == del_node->rc) )
{
// 2.1 删除结点为根结点,则将删除结点的左孩子替代当前删除结点
if (del_node == root)
{
root = root->lc;
}
// 2.2 其他结点,将删除结点的左孩子作为父节点的左孩子
else
{
if (parent_node->lc == del_node)
parent_node->lc = del_node->lc;
else if (parent_node->rc == del_node)
parent_node->rc = del_node->lc;
} delete del_node;
del_node = NULL; dec_size();
} // 3、若删除结点只有右孩子
else if ( (NULL == del_node->lc) && (NULL != del_node->rc) )
{
// 3.1 若为根结点
if (root == del_node)
{
root = root->rc;
}
else
{
if (del_node == parent_node->lc)
parent_node->lc = del_node->rc;
else if (del_node == parent_node->rc)
parent_node->rc = del_node->rc;
} delete del_node;
del_node = NULL; dec_size();
} // 4、若删除结点既有左孩子,又有右孩子,需要找到删除结点的后继结点作为根结点
else if ( (NULL != del_node->lc) && (NULL != del_node->rc) )
{
node *successor_node = del_node->rc;
parent_node = del_node; while (successor_node->lc)
{
parent_node = successor_node;
successor_node = successor_node->lc;
} // 交换后继结点与当前删除结点的数据域
del_node->data = successor_node->data;
// 将指向后继结点的父节点的孩子设置后继结点的右子树
if (successor_node == parent_node->lc)
parent_node->lc = successor_node->rc;
else if (successor_node == parent_node->rc)
parent_node->rc = successor_node->rc; // 删除后继结点
del_node = successor_node;
delete del_node;
del_node = NULL; dec_size();
}
} // 返回以proot为根结点的最小结点
node *get_min_node(node *proot)
{
if (NULL == proot->lc)
return proot; return get_min_node(proot->lc);
} // 返回以proo为根节点的最大结点
node *get_max_node(node *proot)
{
if (NULL == proot->rc)
return proot; return get_max_node(proot->rc);
} // 返回根节点
node *get_root_node()
{
return root;
} // 返回proot结点的父节点
node *get_parent_node(int key)
{
// 当前结点
node *cur_node = NULL;
// 父节点
node *parent_node = NULL; cur_node = root; // 标记是否找到
bool is_find = false;
while (cur_node)
{
if (key == cur_node->data)
{
is_find = true;
break;
} // 因为比当前结点的值还要小,所以需要查找当前结点的左子树
else if (key < cur_node->data)
{
parent_node = cur_node;
cur_node = cur_node->lc;
}
// 同上, 查找当前结点的右子树
else if (key > cur_node->data)
{
parent_node = cur_node;
cur_node = cur_node->rc;
}
} return (true == is_find)? parent_node : NULL;
} private: //查找某个值
node *query_node(node *proot, int key)
{
if (NULL == proot)
{
return proot;
} if (proot->data == key)
return proot;
else if (proot->data > key)
{
return query_node(proot->lc, key);
}
else if (proot->data < key)
{
return query_node(proot->rc, key);
} return NULL;
} // 后序遍历删除所有结点
void remove_all(node *proot)
{
if (NULL != proot)
{
remove_all(proot->lc);
remove_all(proot->rc);
delete proot; dec_size();
}
} // 先序遍历
void pre_order_traverse(node *proot)
{
if (NULL != proot)
{
cout << proot->data << ", ";
pre_order_traverse(proot->lc);
pre_order_traverse(proot->rc);
}
} // 中序遍历
void in_order_traverse(node *proot)
{
if (NULL != proot)
{
in_order_traverse(proot->lc);
cout << proot->data << ", ";
in_order_traverse(proot->rc);
}
} // 后续遍历
void post_order_traverse(node *proot)
{
if (NULL != proot)
{
post_order_traverse(proot->lc);
post_order_traverse(proot->rc);
cout << proot->data << ", ";
}
} // 插入结点
node *insert(node *proot, int data)
{
// 结点不存在, 则创建
if (NULL == proot)
{
node *new_node = new(std::nothrow) node;
if (NULL != new_node)
{
new_node->data = data;
proot = new_node; // 结点+1;
add_size();
} return proot;
} // 插入值比当前结点值还要小, 则应该插入到当前节点的左边
if (proot->data > data)
{
proot->lc = insert(proot->lc, data);
}
// 插入之比当前结点值还要打,则应该插入到当前结点的右边
else if (proot->data < data)
{
proot->rc = insert(proot->rc, data);
} // 相等,则不插入结点。 return proot;
} // size + 1
void add_size()
{
if (hmax_size_32767 == size)
return ;
size++;
} // size - 1
void dec_size()
{
if ( hmin_size_0 == size)
{
return ;
} size--;
} private:
// 根结点
node *root; // 当前树的结点个数
int size;
}; // 测试代码
int main()
{ bstree tree; //
tree.insert_node(50); tree.insert_node(30);
tree.insert_node(10);
tree.insert_node(0);
tree.insert_node(20);
tree.insert_node(40); tree.insert_node(70);
tree.insert_node(90);
tree.insert_node(100);
tree.insert_node(60);
tree.insert_node(80); // 前序遍历
cout << "前序遍历" << endl;
tree.pre_order();
cout << endl; // 中序遍历
cout << "中序遍历" << endl;
tree.in_order();
cout << endl; // 后序遍历
cout << "后序遍历" << endl;
tree.post_order();
cout << endl; cout << "删除结点开始,结束请输入10086" << endl; int del_key = 0; while (true)
{
cout << "输入删除结点值 = ";
cin >> del_key;
if (10086 == del_key)
break; tree.remove_node(del_key); cout << "删除后,结点个数 = " << tree.get_size() << endl;
cout << "删除后, 中序遍历结果:" ;// << endl;
tree.in_order();
cout << endl << endl;
} tree.remove_all(); return 0;
}
测试结果:
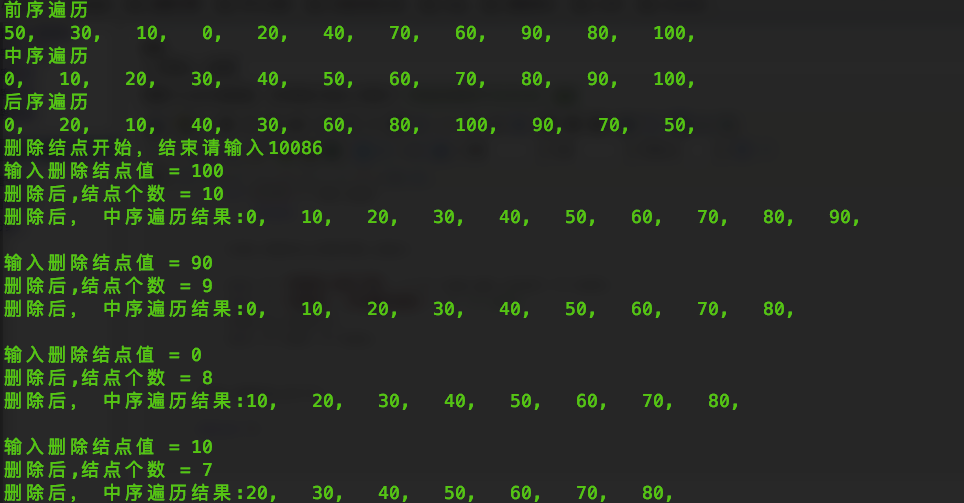
二叉树c++实现的更多相关文章
- [数据结构]——二叉树(Binary Tree)、二叉搜索树(Binary Search Tree)及其衍生算法
二叉树(Binary Tree)是最简单的树形数据结构,然而却十分精妙.其衍生出各种算法,以致于占据了数据结构的半壁江山.STL中大名顶顶的关联容器--集合(set).映射(map)便是使用二叉树实现 ...
- 二叉树的递归实现(java)
这里演示的二叉树为3层. 递归实现,先构造出一个root节点,先判断左子节点是否为空,为空则构造左子节点,否则进入下一步判断右子节点是否为空,为空则构造右子节点. 利用层数控制迭代次数. 依次递归第二 ...
- c 二叉树的使用
简单的通过一个寻找嫌疑人的小程序 来演示二叉树的使用 #include <stdio.h> #include <stdlib.h> #include <string.h& ...
- Java 二叉树遍历右视图-LeetCode199
题目如下: 题目给出的例子不太好,容易让人误解成不断顺着右节点访问就好了,但是题目意思并不是这样. 换成通俗的意思:按层遍历二叉树,输出每层的最右端结点. 这就明白时一道二叉树层序遍历的问题,用一个队 ...
- 数据结构:二叉树 基于list实现(python版)
基于python的list实现二叉树 #!/usr/bin/env python # -*- coding:utf-8 -*- class BinTreeValueError(ValueError): ...
- [LeetCode] Path Sum III 二叉树的路径和之三
You are given a binary tree in which each node contains an integer value. Find the number of paths t ...
- [LeetCode] Find Leaves of Binary Tree 找二叉树的叶节点
Given a binary tree, find all leaves and then remove those leaves. Then repeat the previous steps un ...
- [LeetCode] Verify Preorder Serialization of a Binary Tree 验证二叉树的先序序列化
One way to serialize a binary tree is to use pre-oder traversal. When we encounter a non-null node, ...
- [LeetCode] Binary Tree Vertical Order Traversal 二叉树的竖直遍历
Given a binary tree, return the vertical order traversal of its nodes' values. (ie, from top to bott ...
- [LeetCode] Binary Tree Longest Consecutive Sequence 二叉树最长连续序列
Given a binary tree, find the length of the longest consecutive sequence path. The path refers to an ...
随机推荐
- 洛谷 P3688 - [ZJOI2017]树状数组(二维线段树+标记永久化)
题面传送门 首先学过树状数组的应该都知道,将树状数组方向写反等价于前缀和 \(\to\) 后缀和,因此题目中伪代码的区间求和实质上是 \(sum[l-1...n]-sum[r...n]=sum[l-1 ...
- Codeforces 1458E - Nim Shortcuts(博弈论+BIT)
Codeforces 题目传送门 & 洛谷题目传送门 首先看到这样的题我们不妨从最特殊的情况入手,再逐渐推广到一般的情况.考虑如果没有特殊点的情况,我们将每个可能的局面看作一个点 \((a,b ...
- GWAS分析结果中pvalue/p.ajust为0时如何处理?
在GWAS分析的结果中,偶尔会遇到到pvalue为0的SNP位点,这时如果直接做曼哈顿或QQ图,会出错,因为log0无意义. 此时,该如何处理? 如果你用的是Plink1.9来做的GWAS,可加一个参 ...
- 学习java的第五天
一.今日收获 1.java程序设计完全手册第一章节的小总结 2.完成了部分例题验证解答. 二.今日难题 1.java语言与c++语言的不同点. 2.有例题验证不出来 三.明日目标 1.复习java程序 ...
- acquire, acre, across
acquire An acquired taste is an appreciation [鉴赏] for something unlikely to be enjoyed by a person w ...
- 数仓day01
1. 该项目适用哪些行业? 主营业务在线上进行的一些公司,比如外卖公司,各类app(比如:下厨房,头条,安居客,斗鱼,每日优鲜,淘宝网等等) 这类公司通常要针对用户的线上访问行为.消费行为.业务操作行 ...
- 图形学3D渲染管线学习
图形学3D渲染管线 DX和OpenGL左右手坐标系不同,会有一些差距,得出的矩阵会不一样; OpenGL的投影平面不是视景体的近截面: 顶点(vertexs) 顶点坐标,颜色,法线,纹理坐标(UV), ...
- entfrm-app赋能entfrm零代码开发平台 开启多平台分发
entfrm-app是基于uni-app 框架.使用 Vue.js 语法开发的移动端 App开源产品.它可以编译为 H5.IOS App.Android App.微信小程序.QQ小程序.钉钉小程序.支 ...
- 【Java 8】 Reduce方法
一:reduce rudece方法:从一个流中生成一个值 三个重载方法: Optional<T> reduce(BinaryOperator<T> accumulator); ...
- 使用frp进行内网穿透,实现ssh远程访问Linux服务器
搭建一个完整的frp服务链需要: VPS一台(也可以是具有公网IP的实体机) 访问目标设备(就是你最终要访问的设备) 简单的Linux基础(如果基于Linux配置的话) 我这里使用了腾讯云服务器作为服 ...
