Node.js安装中出现的问题及其解决方案

Node.js安装与配置流程，请参考

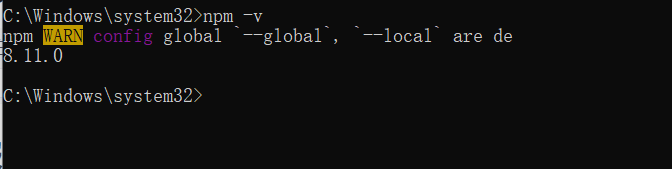
1、npm -v测试时出现警告

更好的选择是安装一个更完善的版本

问题出现的原因 node更新后是最新版 但是npm的版本没有相应的更新存在版本滞后导致问题出现

解决方案如下：

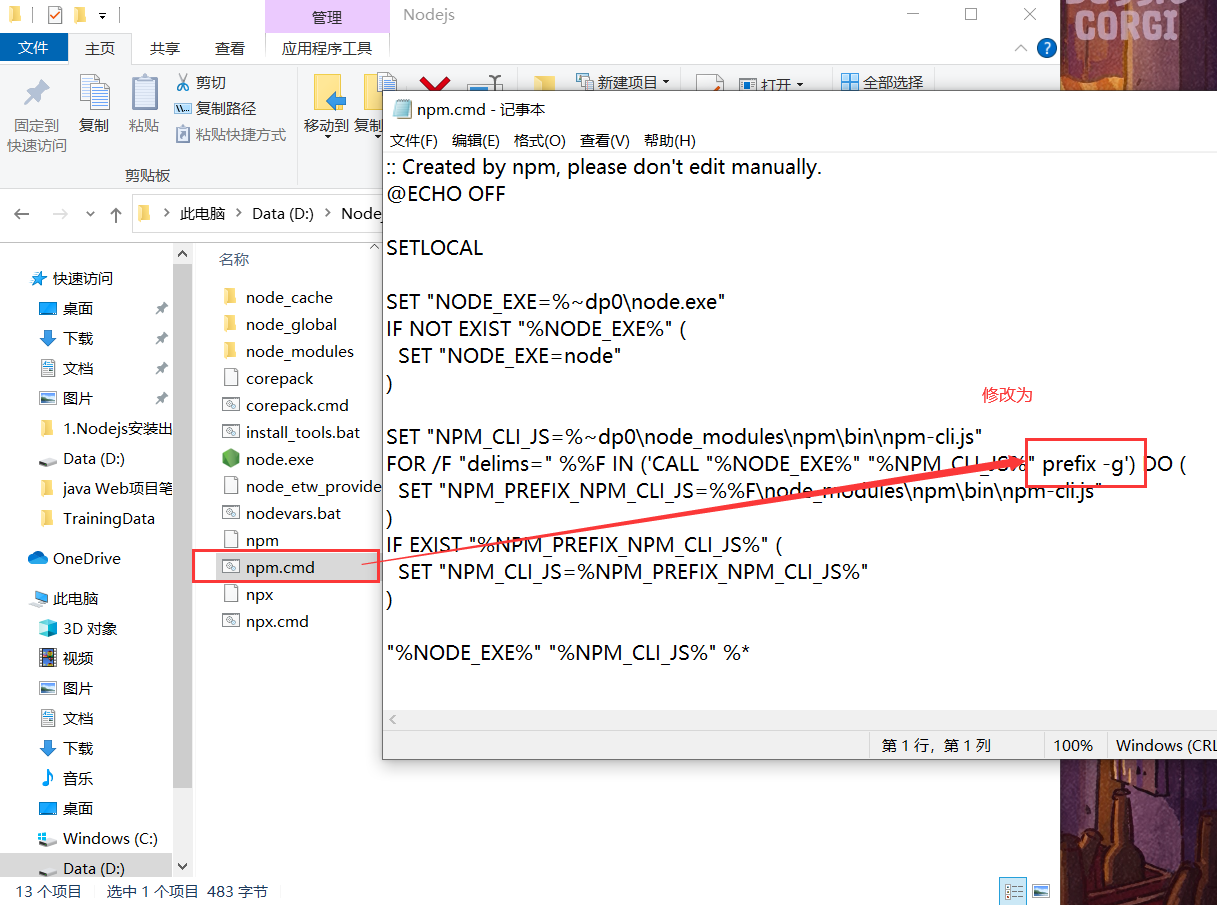
只需要将本地node文件夹中的 npm 和npm.cmd 文件中的 “prefix -g"修改为"prefix --location=global”,保存即可

错误内容如下：

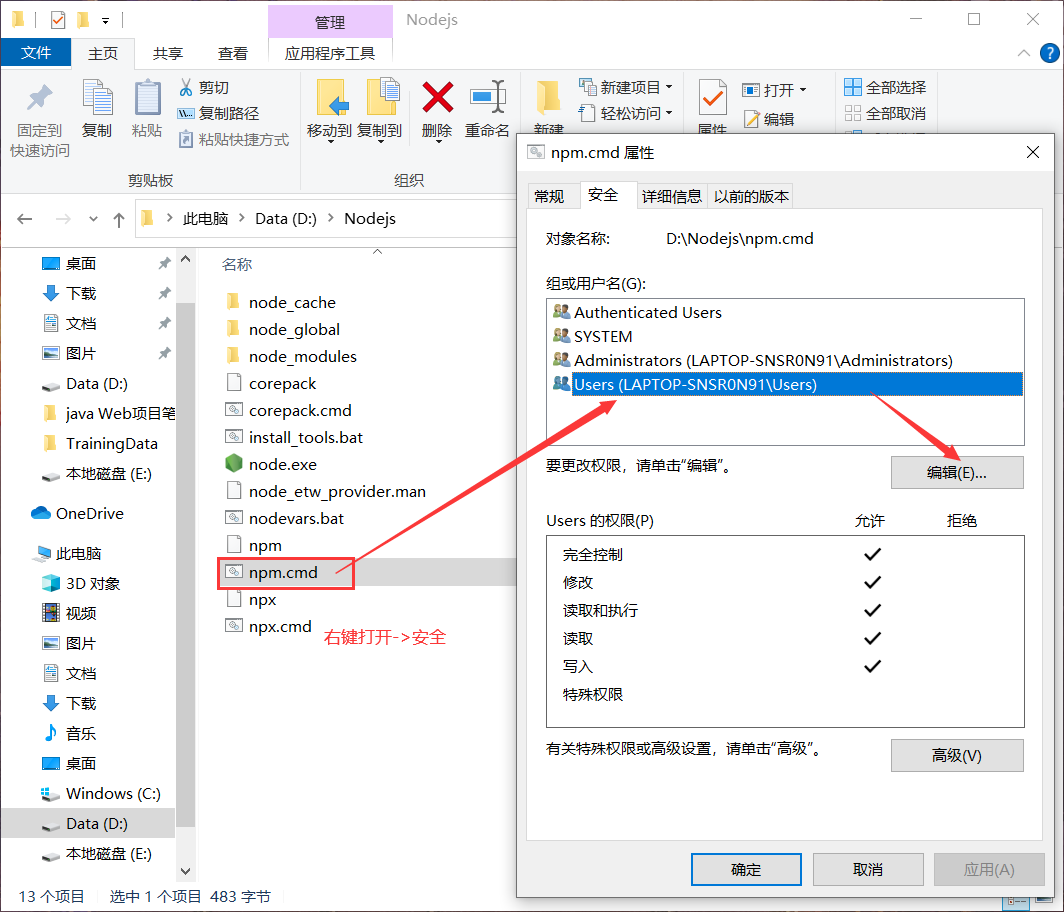
修改流程如下

1、修改权限

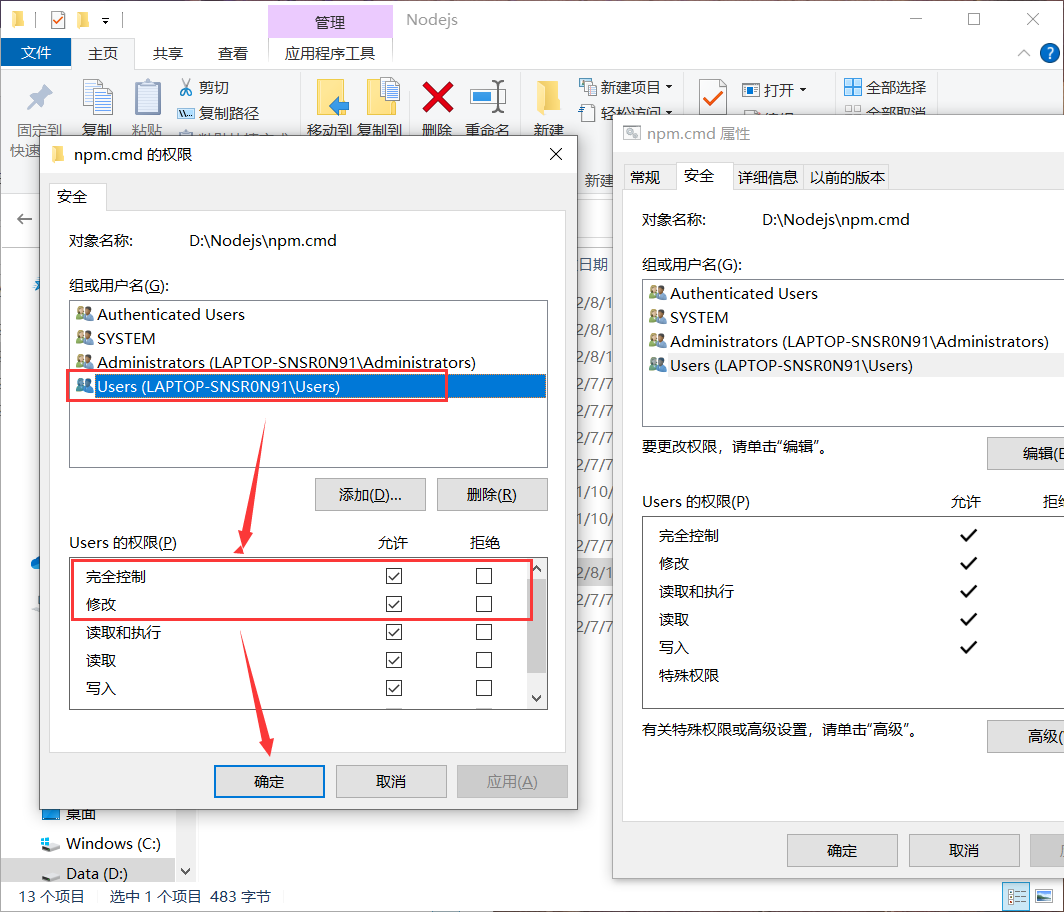
2、修改文件夹内容

2、报错表示权限不够

错误内容：

原因：Win10新增了安全权限插件，对权限的限制更加严格

解决方案：要采用管理员方式运行cmd来执行命令

3、Vue脚手架安装成功后 Vue list执行不成功的问题

原因： Vue list只有在Nodejs安装目录下打开的cmd页面中才可以执行成功