神经网络优化篇：详解梯度检验（Gradient checking）

梯度检验

梯度检验帮节省了很多时间，也多次帮发现backprop实施过程中的bug，接下来，看看如何利用它来调试或检验backprop的实施是否正确。

假设的网络中含有下列参数，\(W^{[1]}\)和\(b^{[1]}\)……\(W^{[l]}\)和\(b^{[l]}\)，为了执行梯度检验，首先要做的就是，把所有参数转换成一个巨大的向量数据，要做的就是把矩阵\(W\)转换成一个向量，把所有\(W\)矩阵转换成向量之后，做连接运算，得到一个巨型向量\(\theta\)，该向量表示为参数\(\theta\)，代价函数\(J\)是所有\(W\)和\(b\)的函数，现在得到了一个\(\theta\)的代价函数\(J\)（即\(J(\theta)\)）。接着，得到与\(W\)和\(b\)顺序相同的数据，同样可以把\(dW^{[1]}\)和\({db}^{[1]}\)……\({dW}^{[l]}\)和\({db}^{[l]}\)转换成一个新的向量，用它们来初始化大向量\(d\theta\)，它与\(\theta\)具有相同维度。

同样的，把\(dW^{[1]}\)转换成矩阵，\(db^{[1]}\)已经是一个向量了，直到把\({dW}^{[l]}\)转换成矩阵，这样所有的\(dW\)都已经是矩阵，注意\(dW^{[1]}\)与\(W^{[1]}\)具有相同维度，\(db^{[1]}\)与\(b^{[1]}\)具有相同维度。经过相同的转换和连接运算操作之后，可以把所有导数转换成一个大向量\(d\theta\)，它与\(\theta\)具有相同维度，现在的问题是\(d\theta\)和代价函数\(J\)的梯度或坡度有什么关系？

这就是实施梯度检验的过程，英语里通常简称为“grad check”，首先，要清楚\(J\)是超参数\(\theta\)的一个函数，也可以将J函数展开为\(J(\theta_{1},\theta_{2},\theta_{3},\ldots\ldots)\)，不论超级参数向量\(\theta\)的维度是多少，为了实施梯度检验，要做的就是循环执行，从而对每个\(i\)也就是对每个\(\theta\)组成元素计算\(d\theta_{\text{approx}}[i]\)的值，使用双边误差，也就是

\(d\theta_{\text{approx}}\left[i \right] = \frac{J\left( \theta_{1},\theta_{2},\ldots\theta_{i} + \varepsilon,\ldots \right) - J\left( \theta_{1},\theta_{2},\ldots\theta_{i} - \varepsilon,\ldots \right)}{2\varepsilon}\)

只对\(\theta_{i}\)增加\(\varepsilon\)，其它项保持不变，因为使用的是双边误差，对另一边做同样的操作，只不过是减去\(\varepsilon\)，\(\theta\)其它项全都保持不变。

之前了解到这个值（\(d\theta_{\text{approx}}\left[i \right]\)）应该逼近\(d\theta\left[i \right]\)=\(\frac{\partial J}{\partial\theta_{i}}\)，\(d\theta\left[i \right]\)是代价函数的偏导数，然后需要对i的每个值都执行这个运算，最后得到两个向量，得到\(d\theta\)的逼近值\(d\theta_{\text{approx}}\)，它与\(d\theta\)具有相同维度，它们两个与\(\theta\)具有相同维度，要做的就是验证这些向量是否彼此接近。

具体来说，如何定义两个向量是否真的接近彼此？一般做下列运算，计算这两个向量的距离，\(d\theta_{\text{approx}}\left[i \right] - d\theta[i]\)的欧几里得范数，注意这里（\({||d\theta_{\text{approx}} -d\theta||}_{2}\)）没有平方，它是误差平方之和，然后求平方根，得到欧式距离，然后用向量长度归一化，使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大，分母使得这个方程式变成比率，实际执行这个方程式，\(\varepsilon\)可能为\(10^{-7}\)，使用这个取值范围内的\(\varepsilon\)，如果发现计算方程式得到的值为\(10^{-7}\)或更小，这就很好，这就意味着导数逼近很有可能是正确的，它的值非常小。

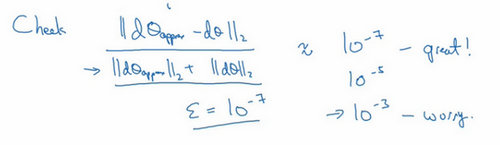
如果它的值在\(10^{-5}\)范围内，就要小心了，也许这个值没问题，但会再次检查这个向量的所有项，确保没有一项误差过大，可能这里有bug。

如果左边这个方程式结果是\(10^{-3}\)，就会担心是否存在bug，计算结果应该比\(10^{- 3}\)小很多，如果比\(10^{-3}\)大很多，就会很担心，担心是否存在bug。这时应该仔细检查所有\(\theta\)项，看是否有一个具体的\(i\)值，使得\(d\theta_{\text{approx}}\left[i \right]\)与$ d\theta[i]$大不相同，并用它来追踪一些求导计算是否正确，经过一些调试，最终结果会是这种非常小的值（\(10^{-7}\)），那么，的实施可能是正确的。

在实施神经网络时，经常需要执行foreprop和backprop，然后可能发现这个梯度检验有一个相对较大的值，会怀疑存在bug，然后开始调试，调试，调试，调试一段时间后，得到一个很小的梯度检验值，现在可以很自信的说，神经网络实施是正确的。