ABC311_g One More Grid Task 题解

题目链接：Atcoder 或者 洛谷

对于解决二维区间内的最值类型问题，我们常常有一类特别好用的方法，就是悬线法，它可以看做是单调栈的子集，但更加好理解和书写。

对于悬线法，我们有一个常见的模型，找出面积最大的符合题意的最大的矩形：

例题 P4147 玉蟾宫。对于悬线法而言，我们需要理解什么是悬线：

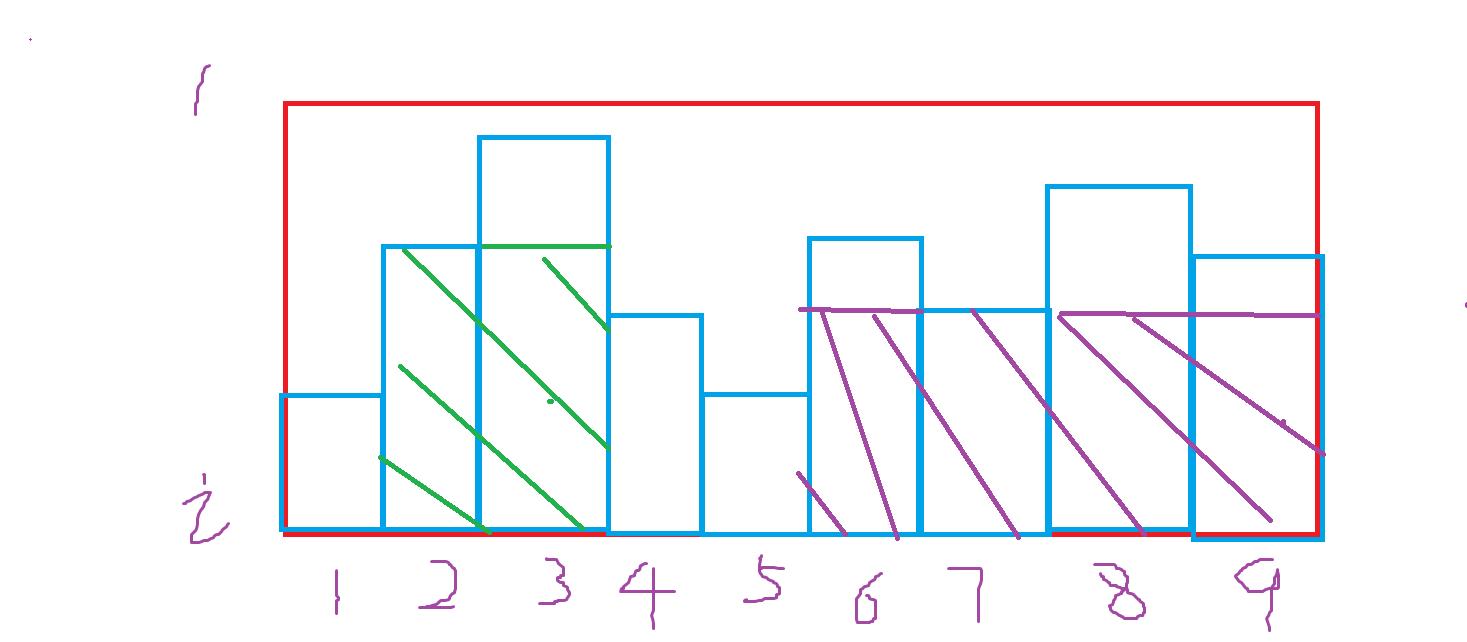
如图所示，我们可以很容易的从第 \(1\) 行往第 \(i\) 行更新的同时，维护从当前行往上满足的最长悬线，在例题当中，则为从当前位置往上的最长连续是 \(F\) 的段。对于以 \(2\) 号位置的上悬线作为高的最优矩形，我们显然要找到它的左右悬线，如图所示，如果它左右两边的上悬线比它高，显然就能拓展出去，使得当前的这根悬线高度不会变小。绿色图形则为最终悬线更新结果。而对于 \(7\) 号上悬线而言，紫色图形则为最终结果。而左右悬线是很好维护求出来的，只需要保证上悬线不减即可，其实这个思想就是类似单调栈思想了，找到左右最先小于自身的端点，但单调栈书写这个逻辑要略显复杂一丢丢，在弹栈时去判断，我们可以用一种更为简单的方法：

更新左右悬线参照代码

forn(j, 1, m)while (L[j] > 1 and h[L[j] - 1] >= h[j])L[j] = L[L[j] - 1];
forv(j, m, 1)while (R[j] < m and h[R[j] + 1] >= h[j])R[j] = R[R[j] + 1];

从左往右更新左悬线，如果比上一个左悬线对应的上悬线还小，那就可以继续拓展到上一个左悬线可以拓展到的左悬线，右悬线就倒序遍历，同理。建议将本题反复练熟再回到原问题上。

至此，回到原题，考虑如何将本题转化为基本的悬线法模型：

很显然的是，本地比较难以处理的是这个区间最小值如何处理，我们注意到区间最小值的数量不超过 \(N\)，而 \(N\) 仅仅为 \(300\)，所以我们可以考虑枚举最小值是多少，那么这样一来，每个点对最小值而言只有两种情况：

1. 如果 \(a[i][j] \ge Value_{min}\)，那么很显然对应的其实就是例题的 \(==F\)。

2. 如果 \(a[i][j] < Value_{min}\)，很显然就是对应的 \(==R\)。

问题转变为原例题问题，找到最大的全为 \(F\) 的矩形，然后答案为这个矩形内的数之和乘上我们枚举的最小值。而求区间和问题，可以预处理出前缀和解决。所以问题至此解决。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize("Ofast,unroll-loops")
// #pragma GCC optimize(2)

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 310;
ll pre[N][N];
int h[N], L[N], R[N];//上悬线的长度,左右悬线的位置
//二维前缀和求区间和
inline ll query(const int x1, const int y1, const int x2, const int y2)
{
    return pre[x2][y2] - pre[x1 - 1][y2] - pre[x2][y1 - 1] + pre[x1 - 1][y1 - 1];
}

int n, m;
ll ans;
int a[N][N];
//悬线法解决最小值为val的答案
inline ll getAns(const ll val)
{
    ll res = 0;
    fill_n(h + 1, m, 0); //每个点上悬线长度初始化为0
    forn(i, 1, n)
    {
        forn(j, 1, m)
        {
            if (a[i][j] >= val)h[j]++;//符合扩展条件,上悬线长度增加
            else h[j] = 0;//不符合扩展条件,没有上悬线
            L[j] = R[j] = j;//初始化当前列的左右悬线
        }
        forn(j, 1, m)while (L[j] > 1 and h[L[j] - 1] >= h[j])L[j] = L[L[j] - 1];
        forv(j, m, 1)while (R[j] < m and h[R[j] + 1] >= h[j])R[j] = R[R[j] + 1];
        forn(j, 1, m)if (h[j])uMax(res, query(i - h[j] + 1, L[j], i, R[j]) * val);//有上悬线就计算答案
    }
    return res;
}

int mx;

inline void solve()
{
    cin >> n >> m;
    forn(i, 1, n)
    {
        forn(j, 1, m)
        {
            cin >> a[i][j];
            uMax(mx, a[i][j]), pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + a[i][j];
        }
    }
    forn(i, 1, mx)uMax(ans, getAns(i));//枚举最小值
    cout << ans;
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度为枚举最小值乘上单次悬线法处理复杂度: \ O(value_{max} \times nm)
\]

总结：

关于悬线法而言，它常常会与二维区间的最优矩形查找有关。而我们实际上需要转化为普通悬线法的模型，需要优先考虑上悬线的扩展条件，对于某一个点而言，如果它的上悬线的扩展条件固定了，那么左右条件悬线扩展就很轻松了。建议反复将例题进行熟悉，这样遇到其他的其他的题型也可以转化为最本质的模型去解决。