Codeforces Global Round 1 解题报告

A

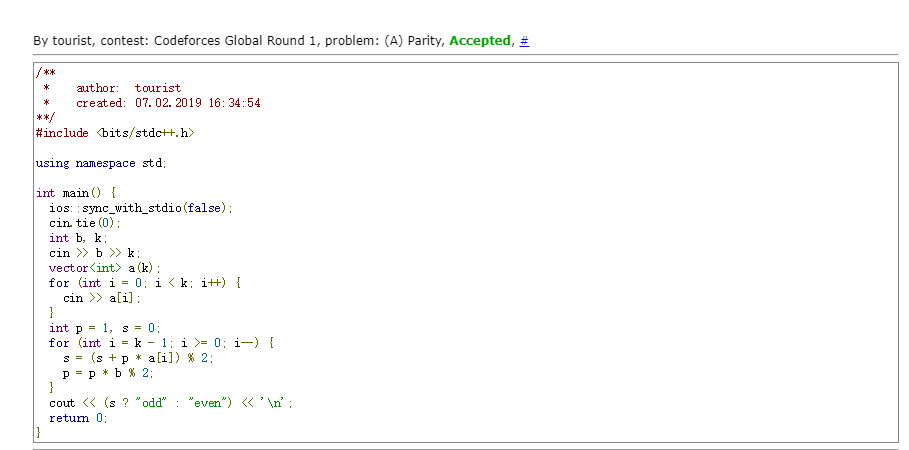
我的方法是：

#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
const int N=2e5+100;
const int INF = 1e9;

int32_t main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int b, k;
    cin >> b >> k;
    int sum = 0;
    int a[N];
    for (int i = 0; i < k;i++){
        cin >> a[i];
        a[i] = a[i] % 2;
        sum += a[i];
    }
    if(b%2==0){
        if(a[k-1]==1)
            cout << "odd";
        else
        cout << "even";
        //system("pause");
        return 0;
    }
    else{
        if(sum%2==0)
            cout << "even";
        if(sum%2)
            cout << "odd";
    }
    //system("pause");
    return 0;
}

如果b是奇数，那么必须保证系数A相加是偶数，结果才能是偶数
如果b是偶数，那么只要看最后的常数项是奇数还是偶数

B

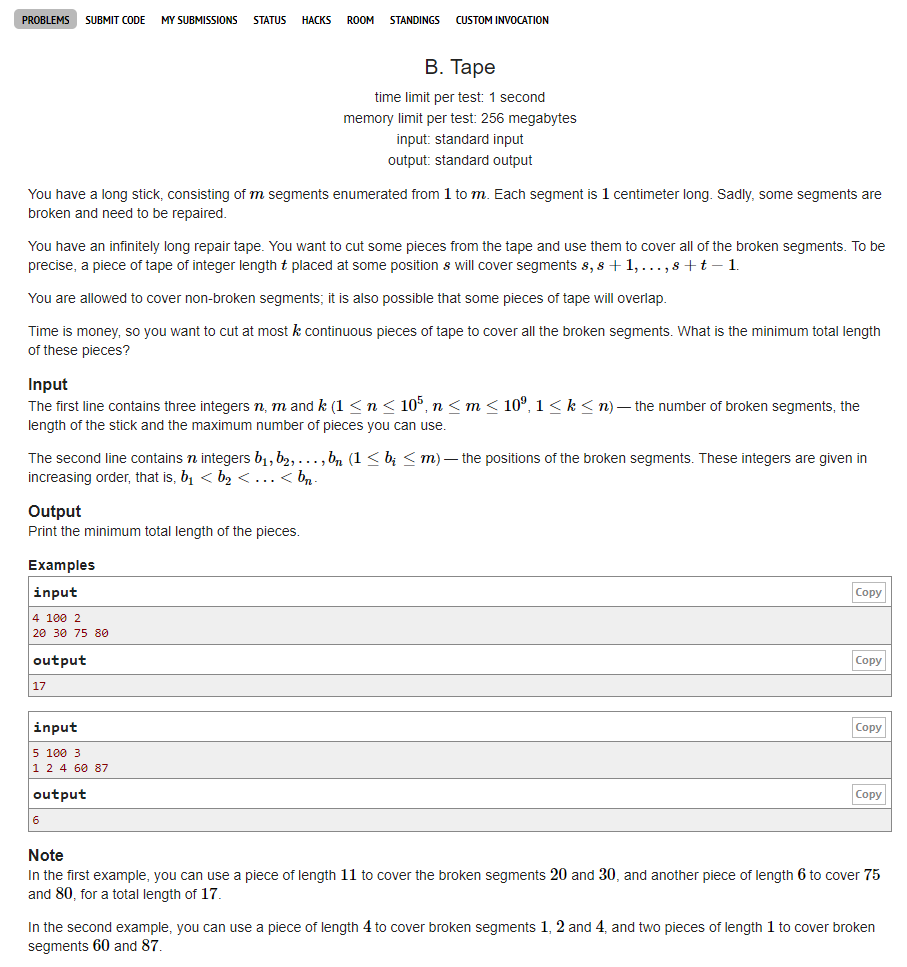
B题：

C

C题

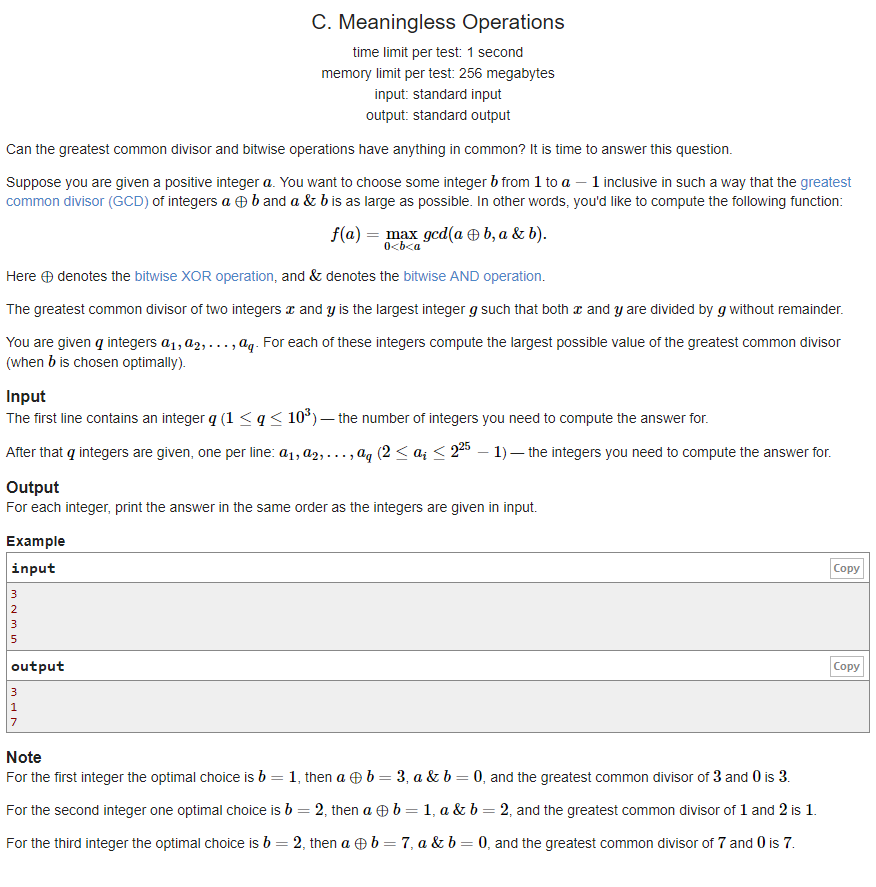
这个C题，
只是因为在人群中多看了你一眼，我脑壳痛到现在

好了好了我脑壳不痛了，我们开始分析吧！！！
首先我们要搞清楚XOR 和 AND的操作是什么意思
XOR就是异或（^）同0异1
AND就是与（&）都1则1，有0则0
比如说现在有个数，是9
我们还要知道，一般想要gcd(a,b)取得最大值，比如gcd(a,b)==a,那么b==0；
所以对于题目里的
f(a)=max gcd(a^b,a&b);
我们已经知道a了，现在要选取一个合适的b
想要得到一个最大值，那么可以考虑让a&b==0，然后，再求a^b，这个a^b就是答案
举例1：
9的二进制是：1001
假设一个b 使得9&b==0，那么b==0110，也就是6
b==6时，9^b==9^6==1111
对于一个四位的二进制来说，1111是最大值

样例里的3
3(10)==11(2)
3的各位都是1，那么此时b又不能为0，咋办？
打表~~
对于所有为2^n-1的数，打表求它们的最大公因子就ok了

另外还有
2pow4-1=2(2pow3-1)+1;

发现了很棒的代码
https://www.cnblogs.com/shanxieng/p/10355918.html

E

E题，差分数组
刚看到差分数组的定义，我心想，这跟线段树有个啥区别
后来才知道，一个始用于"离线“，另一个始用于”在线"
也就是，差分数组最好是update完了再一起查询
线段树就随便了，什么时候都ok
然后还有一句话:
D[]是A[]的差分数组，A[]是D[]的前缀和

举个栗子
a1 a2 a3 a4
a2=a1+a3-a2;
d2=a3-a2=a3-(a1+a3-a2)=a2-a1=d1;
d2=d1,多么神奇！