支持向量机SVM 简要推导过程

SVM 是一块很大的内容，网上有写得非常精彩的博客。这篇博客目的不是详细阐述每一个理论和细节，而在于在不丢失重要推导步骤的条件下从宏观上把握 SVM 的思路。

1. 问题由来

SVM (支持向量机) 的主要思想是找到几何间隔最大的超平面对数据进行正确划分，与一般的线性分类器相比，这样的超平面理论上对未知的新实例具有更好的分类能力。公式表示如下：

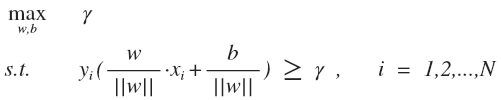
$\gamma$ : 所有点中最小的几何间隔, 实际上就是支持向量上的点的几何间隔

$x_i,y_i$ : 训练样本及对应标签， $y_i\in \{-1,+1\}$ , 作用是将第 i 个样本点的几何间隔转化为正数

公式的意思是假设每个训练样本点的几何间隔至少是 $\gamma$ , 求 $\gamma$ 的最大值。

由于几何间隔（没帽子）和函数间隔（有帽子）的关系是：

$\gamma = \frac{\hat{\gamma}}{||w||}$

最大化 $\gamma$ 可以固定 $\hat{\gamma}$ ,求 ||w|| 的最小值或者固定 ||w||, 求 $\hat{\gamma}$ 的最大值，一般选择前者: 固定函数间隔为 1, 将 \gamma = 1/||w|| 带入上式，同时为了计算方便，目标函数等价于最小化 ||w||^2 ,约束优化问题转化为：

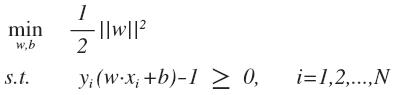
这是一个 QP 优化问题。

2. 对偶问题

利用拉格朗日乘子法将约束条件融入到目标函数:

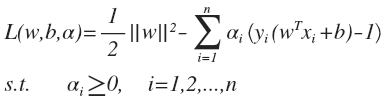
SVM 的原始问题实际上是一个极小极大问题：

这个表达式有几个变量，先从哪一个着手？答案是 $\alpha$ , 至于为什么，实际上是根据下面这个优化函数将原始问题的约束条件——函数间隔必须不小于 1 转化到拉格朗日乘子 $\alpha$ 向量上去的，先看函数的后面一部分：

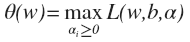
很容易可以看出，如果样本点 xi 满足约束条件，即有 $y_i(w^Tx_i+b)-1\ge 0$ , 上式求最大，必定有 $\alpha_i(y_i(w^Tx_i+b)-1)=0$ , alpha 与后面括号里面的式子必有一个为 0 (VI) 所有的样本点都满足约束条件，极小极大问题就转化为 $\min_{w,b}{\frac{1}{2}\| w\| ^2}$ , 如果有一个样本点不满足约束条件，alpha 值取无穷大，上式将取无穷大，显然是没有意义的。实际上，这段论述就说明了原始问题具有 KKT 强对偶条件，对于原始问题来说需要满足的 KKT 条件有哪些呢？

$\alpha _i^*(y_i(w^{*T}x_i + b^* - 1)) = 0$
$y_i(w^{*T}x_i + b^* - 1)\ge 0$
$\alpha ^*\ge 0$

倒数两个条件是原始问题的条件，肯定成立。第一个条件是上面讨论过的条件:

当样本不在支持向量上，alpha 一定等于 0, w 在不等式2的内部，这是一个松的约束，L 函数就等于 1/2||w||^2 ，取它的偏导为0就可以了。
当样本点在支持向量上时， w 在不等式2的边界上，这是一个等式约束，这就和普通的拉格朗日等式约束相同，在最优点目标函数和约束条件函数的导数平行。用 wiki 的一张图来表示：

原始问题满足 KKT 条件，可以转化成一个最优解等价的对偶极大极小问题，先对极小部分求偏导：

得到对偶最优化问题：

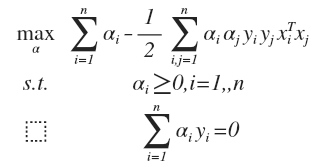
对于一个新来的样本，将上面 w 的值带入 f(x) = w^T·x + b，可以知道要判断新来的点，我们只需要计算它与训练点的内积即可，这是 kernel trick 的关键：

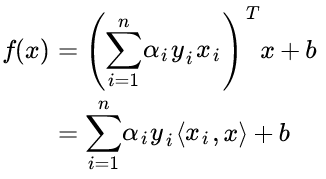
3. 软间隔

软间隔问题是应对 outliers 的一种方法。软间隔问题可以建立目标函数：

与硬间隔的优化方法相似，得到的解是：

4. Kernel Method

核方法是一种很巧妙的方法，既可以将特征映射到较高的维度，又可以地利用了 SVM 的内积运算避免了维度计算量的爆炸。最后的最优化问题与硬间隔优化问题相似，只要将两个样本的内积改为两个样本的核函数即可 (kernel substitution) ：

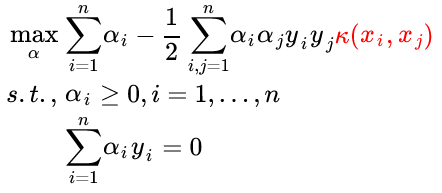
当然，你也可以将两个样本的内积看做最简单的核函数。Kernel method 不仅可以用在 SVM 上，还可以用在 PCA、线性分类器上等，以后再专门写一篇 kernel method 的博客。

参考资料：

[1] pluskid 的博客

[2] 统计学习方法，李航著

by：daniel-D

from：http://www.cnblogs.com/daniel-D/