cordic算法的fpga实现

cordic算法参考：http://wenku.baidu.com/view/6c623aa8910ef12d2bf9e732.html

这是百度文库的一个文档，详细介绍了cordic算法的基本内容。我就是读了这个文档后做的cordic算法实现sin cos的运算的。

先谈感悟：做这种迭代型的算法，我觉得用for语句实现是最容易理解的，所以我的设计就是基于for结构实现的，关于算法中重要的位数确定，上边的文档里也有说明，我的选择是z选17位，1位符号位，8位整数，8位小数，x，y选21位，20位小数，一位符号位。所有数都是照这个标准的。

贴代码(贴后格式改变了，没缩进了，凑合看)

module test_cordic(clk,rst_n,z0,en,sin_out,cos_out);//z0是输入角度值，en是运算使能，sin_out,cos_out是运算输出。

input clk,rst_n;
input [16:0] z0;
input en;
output [10:0] sin_out,cos_out;
reg en_buff;
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)
en_buff<=0;
else
en_buff<=en;
end
reg [16:0] angel[0:9];
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
angel[0]<=17'b00010110100000000;//45
angel[1]<=17'b00001101010011001;//26.6
angel[2]<=17'b00000111000000000;//14
angel[3]<=17'b00000011100011001;//7.1
angel[4]<=17'b00000001110011001;//3.6
angel[5]<=17'b00000000111001100;//1.8
angel[6]<=17'b00000000011100110;//0.9
angel[7]<=17'b00000000001100110;//0.4
angel[8]<=17'b00000000000110011;//0.2
angel[9]<=17'b00000000000011001;//0.1
end
end

reg [16:0]reg_z[0:9];//1 fuhao wei 8 zhengshu 8xiaoshu
reg [10:0] reg_x[0:9];
reg [10:0] reg_y[0:9];
reg [4:0] i;
always@(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
for(i=0;i<=9;i=i+1'b1)
begin
reg_x[i]<=0;
reg_y[i]<=0;
reg_z[i]<=0;
end
end
else if(en&&!en_buff)
begin
reg_x[0]<=11'b01001101101;//0.6073<<10 + 1wei fuhao wei
reg_y[0]<=0;
reg_z[0]<=z0;
end
else
begin
for(i=1;i<=9;i=i+1'b1)
begin
if(reg_z[i-1][16])
begin
reg_x[i]<=reg_x[i-1]+(reg_y[i-1]>>i-1);
reg_y[i]<=reg_y[i-1]-(reg_x[i-1]>>i-1);
reg_z[i]<=reg_z[i-1]+angel[i-1];
end
else
begin
reg_x[i]<=reg_x[i-1]-(reg_y[i-1]>>i-1);
reg_y[i]<=reg_y[i-1]+(reg_x[i-1]>>i-1);
reg_z[i]<=reg_z[i-1]-angel[i-1];
end
end
end
end
assign sin_out=reg_y[9];
assign cos_out=reg_x[9];
endmodule

测试代码较简单，不贴了，贴一个30度求值结果

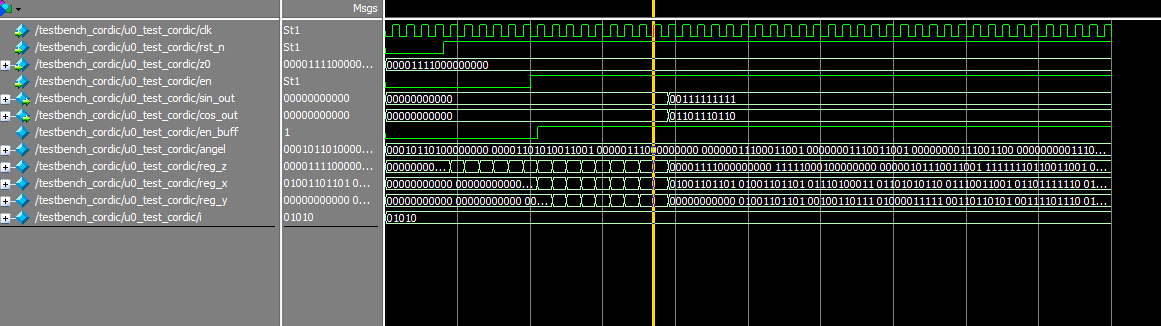
结果是sin30=00111111111；什么意思？最高位符号位是0，代表正数，后10位是小数部分即0.0111111111；转为10进制就是0.499；同理cos30=01101110110转为10进制就是0.8652.当然也可以试试其他角度。