HDU 6090 Rikka with Graph —— 2017 Multi-University Training 5

Rikka with Graph

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Problem Description

As we know, Rikka is poor at math. Yuta is worrying about this situation, so he gives Rikka some math tasks to practice. There is one of them:

For an undirected graph G with n nodes and m edges, we can define the distance between (i,j) (dist(i,j)) as the length of the shortest path between i and j. The length of a path is equal to the number of the edges on it. Specially, if there are no path between i and j, we make dist(i,j) equal to n.

Then, we can define the weight of the graph G (wG) as ∑ni=1∑nj=1dist(i,j).

Now, Yuta has n nodes, and he wants to choose no more than m pairs of nodes (i,j)(i≠j) and then link edges between each pair. In this way, he can get an undirected graph G with n nodes and no more than m edges.

Yuta wants to know the minimal value of wG.

It is too difficult for Rikka. Can you help her?

In the sample, Yuta can choose (1,2),(1,4),(2,4),(2,3),(3,4).

 

Input

The first line contains a number t(1≤t≤10), the number of the testcases.

For each testcase, the first line contains two numbers n,m(1≤n≤106,1≤m≤1012).

 

Output

For each testcase, print a single line with a single number -- the answer.

 

Sample Input

1
4 5

 

Sample Output

14

题意:有n各点，问取其中至多m对点连成边，每条边的权值为1，求连好之后所有点之间的最短路（记为dis(i,j)）的和的最小值。若两个点不是连通的，则这两条边的dis取作n。

思路：贪心。

1.当m<=n-1时，我们尽可能每一条边都把不同的点连通，我们可以把 ① 点作为根节点，每加入一条边，就从这个根节点连接到另一个不在连通块里的点(见下图，虚线代表下一条连接的边)。

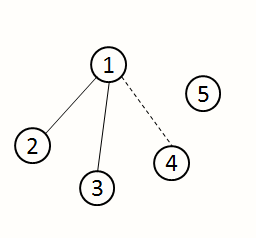
对于被连接的点来说，它到根节点的距离从 n -> 1, 到其他在子节点的距离从 n -> 2, 所以加入第 i 个点后，原先总距离之和减少了 2*[（n-1）+(i-1)*(n-2)]。由于m=0(即没有边)时总距离和为 n*n*(n-1), 此时总距离和为

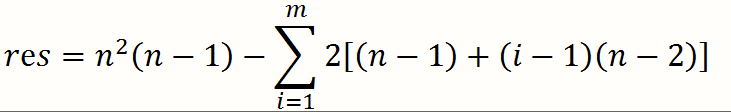
2.当m>n-1时，剩余的点两两相连，由于每两个子节点之间距离都是2，每连一条边都只有一对点的距离从2变为1，所以每多连一条边，总距离减少 2*1，所以在上式的基础上减去 2*（m-(n-1)） 即可。注意当m > n*(n-1)/2时最多能取n*(n-1)/2对点， res=n*(n-1)。

AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long LL;
int main()
{
    LL n,m;
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%lld %lld", &n, &m);
        LL res=n*n*(n-);
        if(m>){
            if(m<=n-){
                res=res-m*(m-)*(n-)-*m*(n-);
            }
            else if(m>n*(n-)/)
                res=n*(n-);
            else{
                res=res-(n-)*(n-)*(n-)-*(n-)*(n-)-*(m-n+);
            }
        }
        printf("%lld\n", res);
    }
    return ;
}