题解 P2674 【《瞿葩的数字游戏》T2-多边形数】

题目说了很清楚，此题找规律，那么就找规律。

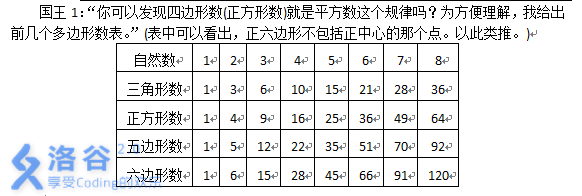
我们观察数列。

令k表示数列的第k个数。

---

三角形数：1 3 6 10 15

两项相减：1 2 3 4 5

再次相减：1 1 1 1 1

---

四边形数：1 4 9 16 25

两项相减：1 3 5 7 9

再次相减：2 2 2 2 2

…………

仔细看，第n形数的\(a_k = \sum_{1}^{k}1+(n-2)(k-1)\)

∴\(a_k = [2 + (k-1)(n-2)]k / 2\)

∴\(2a_k = [2 + (k-1)(n-2)]k\)

∴\(4k + k^2 * n - 2 * k^2 - nk = a_k * 2\)

∴\((k^2-k)n = a_k * 2 - 4k + 2k^2\)

∴\(n = \frac{a_k * 2 - 4k + 2k^2}{(k^2-k)}\)

然后枚举k即可。

注意n >= 3.

并且，特判1,2。

代码如下：

#include<bits/stdc++.h>
using namespace std;
int main(){
	int T;
	cin >> T;
	while (T--){
		long long n = 0;
		cin >> n;
		if (n == 1)
			cout << "3 4\n";
		else if (n == 2)
			cout << "Poor2\n";
		else{
			long long fir = 0,sec = 0;
			for (int k=2;k<=n;k++){
				int tpl = (n * 2 - 4 * k + 2 * k * k);
				int tpr = (k * k - k);
				if (tpl < 3 * tpr) break;
				if (tpl % tpr == 0)
					sec = fir, fir = tpl / tpr;
			}
			if (fir == 0)
				cout << "Poor" << n << endl;
			else if (sec == 0)
				cout << fir << endl;
			else cout << fir << ' ' << sec << endl;
		}
	}
}