清北学堂提高组突破营游记day6

还有一天就结束了。。QWQ

好快啊。

昨天没讲完的博弈论DP：

一个标准的博弈论dp，一般问的是是否先手赢。

博弈论最关键的问题：dp过程。

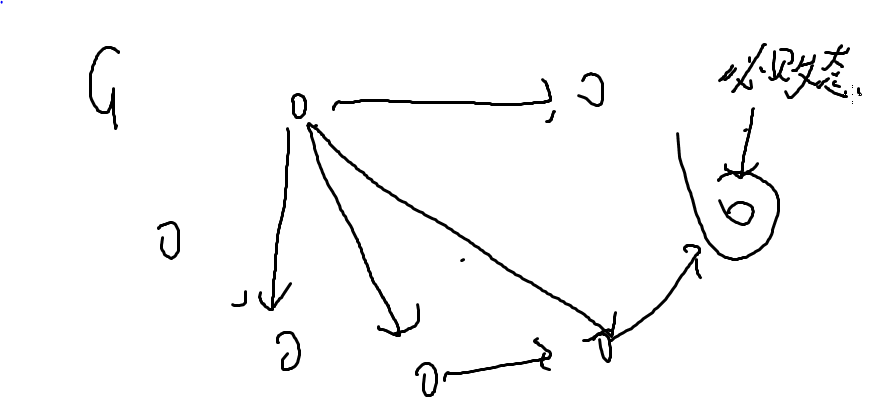
对于一个问题，一定有很多状态，每个状态可以转移到其他的一些状态。如果存在一个状态，且不能转移到其他状态，那么我们设这个状态为必败态，那么他相邻的能够转移到必败态的状态因为只有一种转移方式，那么一定为必胜态，（假设操作双方选手绝顶聪明，每一步都朝着最优状态走），如此这样交替下去，推到开始状态，就可以判断了。

怎么转换？

对于一个节点以及他所有子节点来讲，如果子节点全部为true（对手的必胜态），那么当前节点为你的必败态。

如果子节点中有一个false（对手必败态），那么当前节点就是你的必胜态。

于是我们用dfs记忆化枚举并dp：

#include<iostream>

using namespace std;

bool f[][],g[][];

bool dfs(int i,int j)
{
    if (i==) return false;
    if (g[i][j]) return f[i][j];
    g[i][j]=true;f[i][j]=false;
    for (int r=;r<=i && r<=k*j;r++)
        if (dfs(i-r,r) == false) f[i][j]=true;
    return f[i][j];
}

int main()
{
    cin >> s >> k;
    for (int a=;a<s;a++)
        if (dfs(s-a,a) == false)
        {
            cout << "Alice" << endl;
            return ;
        }
    cout << "Bob" << endl;

    return ;
}

这个题用到sg函数：sg[n]表示从n往下到一个能取到的最低的值中最小的没有出现过的非负整数的值，

suchas：在序列2 5 6 7中，sg[4]=0，在序列1 2 3 4 6中，sg[5]=5；

这个东西有什么用？

SG函数可以解决大多数博弈问题，当然也可以通过SG函数找规律，然后计算结果。

答案是把所有奇数堆都取出来并求sg函数并亦或，如果答案为0，先手必败。

至于sg的正确性的话。。。

zhx：“这个东西如果你去看的话没有2个小时你是看不下来的，如果想看懂全部原理和证明的话没有2天是不行的。”.

我看了看，

所以证个锤子。背过模板万事皆有可能。

各种例题：

sg函数求法：

下午考试，爆零警告。