dijkstra算法之优先队列优化

github地址；https://github.com/muzhailong/dijkstra-PriorityQueue

1.题目

分析与解题思路

dijkstra算法是典型的用来解决单源最短路径的算法，该算法采用贪心的思想，广度优先搜索的策略，每一轮从当前节点找对与其邻接的所有节点进行放松操作（比较距离源点的距离，来决定是否执行），记录当前节点为已访问，之后从所有未访问过的节点中找到距离源点最近的节点作为当前节点，重复上述操作。BFS策略体现在每次从当前节点，访问所有与其邻接的节点；贪心的思想体现在，每一轮之后，当前距离最短的点S被认为不存在从源点到S更短的路径，每次当通过S对与其邻接的节点进行放松后，可以将S从集合剔除，因为通过后续的到达S节点的距离一定更长。

证明：

假设源点为S0，当前节点为S，节点S0到节点u的距离为dis[u];

因为当前节点为S，说明其他节点u！=S，必有dis[u]>dis[S]

假如后续的节点v有一条到S的路径，源点到v的距离必然是通过S或者u进行放松的

dis[v]>=min{dis[u],dis[S]}

另外dijkstra算法只能解决权值为正的情况，当存在负权值时，算法可能出错，比如：

节点从1开始，根据贪心思想，下一下节点应该选择3，记录dis[3]=2

但是有更短的路径1->2->3 距离为1

测试用例

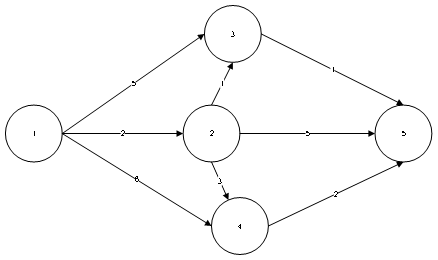
（测试用例1）

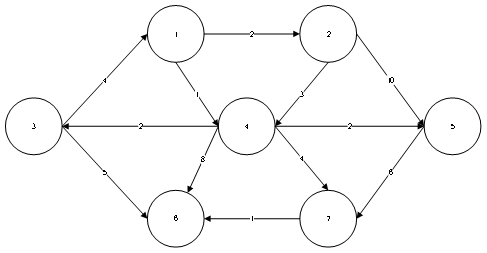
（测试用例2）

输入说明：

第一行：测试用例的数目

对于每一个测试用例，第一行，n,m,s;n代码节点的个数，m代表边的条数，s代码源节点

后面m行，u,v,w代表一条u->v权值为w的边

程序实现

 public List<int[]>dijkstra1(int s)；使用的是课本上比较朴素的实现方法。

下面是我自己的实现方法：

//采用优先队列优化

   public List<int[]>dijkstra2(int s){

        int[]path=new int[n+1];

        int[]dis=new int[n+1];

        boolean[]mark=new boolean[n+1];

        Arrays.fill(dis, INF);

        dis[s]=0;

        path[s]=0;

        PriorityQueue pq=new PriorityQueue(n);

        for(int i=1;i<n;++i) {

            for(Node temp:table.get(s)) {

                if(!mark[temp.index]&&dis[s]+temp.weight<dis[temp.index]) {

                    if(dis[temp.index]==INF) {

                        dis[temp.index]=dis[s]+temp.weight;

                        pq.offer(temp.index, dis[temp.index]);

                    }else {

                        pq.increase(temp.index, dis[s]+temp.weight-dis[temp.index]);

                        dis[temp.index]=dis[s]+temp.weight;

                    }

                    path[temp.index]=s;

                }

            }

            mark[s]=true;

            s=pq.poll();

        }

        ArrayList<int[]>res=new ArrayList<int[]>(2);

        res.add(path);

        res.add(dis);

        return res;

    }

使用优先队列优化，每次寻找最小的距离的节点的时候就不用线性遍历整个表，可以在logV的时间复杂度内获得最小距离的节点；同时我在使用优先队列的时候，我的实现方式对优先队列有以下额外要求：（优先队列的代码有点长，具体情况源代码）

1) 能够更新元素

先找到指定的元素，根据2）中的方法，然后更新dis，如果dis变小进行上滤，dis变大进行下滤。

2) 能够在常数时间内找到在图中某个标号的节点在优先队列中的位置

一个很常见的思路就是使用空间换时间，使用一个数组保存Node在优先队列中的位置，并且在优先队列进行插入，删除，更新时也要同步更新。

运行截图

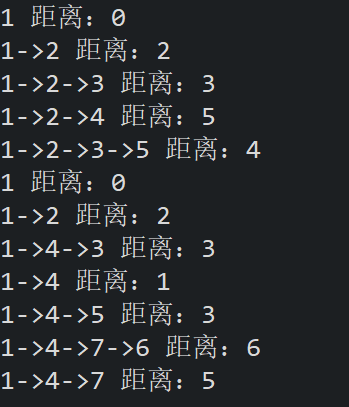
结论

朴素的实现时间复杂度是O（E*V）（我使用的是邻接表存储图），使用优先队列优化时间复杂度为O（VlogV）；关于图的存储，稀疏图使用邻接表占用内存比较少，稠密图适合用邻接矩阵，访问速度很快。