深入理解dijkstra+堆优化

深入理解dijkstra+堆优化

其实就这几种代码几种结构，记住了完全就可以举一反三，所以多记多练多优化多思考。

Dijkstra

 

对于一个有向图或无向图，所有边权为正（边用邻接矩阵的形式给出），给定a和b，求a到b的最短路，保证a一定能够到达b。这条最短路是否一定存在呢？答案是肯定的。相反，最长路就不一定了，由于边权为正，如果遇到有环的时候，可以一直在这个环上走，因为要找最长的，这样就使得路径越变越长，永无止境，所以对于正权图，在可达的情况下最短路一定存在，最长路则不一定存在。这里先讨论正权图的最短路问题。

      最短路满足最优子结构性质，所以是一个动态规划问题。最短路的最优子结构可以描述为：

      D(s, t) = {Vs ... Vi ... Vj ... Vt}表示s到t的最短路，其中i和j是这条路径上的两个中间结点，那么D(i, j)必定是i到j的最短路，这个性质是显然的，可以用反证法证明。

      基于上面的最优子结构性质，如果存在这样一条最短路D(s, t) = {Vs ... Vi Vt}，其中i和t是最短路上相邻的点，那么D(s, i) = {Vs ... Vi} 必定是s到i的最短路。Dijkstra算法就是基于这样一个性质，通过最短路径长度递增，逐渐生成最短路。

      Dijkstra算法是最经典的最短路算法，用于计算正权图的单源最短路（Single Source Shortest Path，源点给定，通过该算法可以求出起点到所有点的最短路），它是基于这样一个事实：如果源点到x点的最短路已经求出，并且保存在d[x] ( 可以将它理解为D(s, x) )上，那么可以利用x去更新 x能够直接到达的点 的最短路。即：

      d[y] = min{ d[y], d[x] + w(x, y) }           y为x能够直接到达的点，w(x, y) 则表示x->y这条有向边的边权

      具体算法描述如下：对于图G = <V, E>，源点为s，d[i]表示s到i的最短路，visit[i]表示d[i]是否已经确定(布尔值)。

      1) 初始化 所有顶点 d[i] = INF, visit[i] = false，令d[s] = 0；

      2) 从所有visit[i]为false的顶点中找到一个d[i]值最小的，令x = i; 如果找不到，算法结束；

      3) 标记visit[x] = true, 更新和x直接相邻的所有顶点y的最短路： d[y] = min{ d[y], d[x] + w(x, y) }

     （第三步中如果y和x并不是直接相邻，则令w(x, y) = INF）

 

实例：

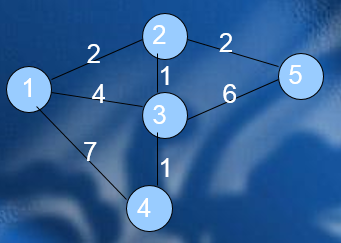
输入：

5 7
1 2 2
2 5 2
1 3 4
1 4 7
3 4 1
2 3 1
3 5 6

 #include <bits/stdc++.h>
 using namespace std;
 int n,m;
 struct node{
     int to;
     int w;
 };
 int edgeNum[];
 vector<node> vec[];
 int dis[];
 bool vis[];

 void addEdge(int a,int b,int w){
     edgeNum[a]++;
     node *p=new node();
     p->to=b;
     p->w=w;
     vec[a].push_back(*p);
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int a,b,w;
         cin>>a>>b>>w;
         addEdge(a,b,w);
         addEdge(b,a,w);
     }
 }

 void dijkstra(int start){
     memset(dis,0x3f,sizeof(dis));
     dis[start]=;
     for(int i=;i<edgeNum[start];i++) {
         int b=vec[start][i].to;
         int w=vec[start][i].w;
         dis[b]=w;
     }
     vis[start]=;
     for(int k=;k<=n-;k++){
         int minV=0x7fffffff,min_i;
         for(int i=;i<=n;i++){
             if(!vis[i]&&dis[i]<minV){
                 minV=dis[i];
                 min_i=i;
             }
         }
         vis[min_i]=true;
         for(int i=;i<edgeNum[min_i];i++){
             int b=vec[min_i][i].to;
             int w=vec[min_i][i].w;
             if(!vis[b]&&dis[b]>dis[min_i]+w){
                 dis[b]=dis[min_i]+w;
             }
         } 

     }

 }

 void print(){
     for(int i=;i<=n;i++)
         cout<<dis[i]<<" ";
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     dijkstra();
     print();
     return ;
 } 

上面的代码说几点：

1、13行到19行的代码可以通过给结构体添加构造函数来优化。

2、dijkstra中的节点如果改成u，v的话更清晰

3、朴素的dijkstra分为如下几步：初始化dis数组，n-1轮（找最优节点，更新）

求节点1到其它节点的距离：

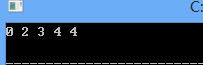
堆优化：

 #include <bits/stdc++.h>
 using namespace std;
 int n,m;
 struct node{
     int to;
     int w;
 };
 int edgeNum[];
 vector<node> vec[];
 int dis[];
 bool vis[];

 void addEdge(int a,int b,int w){
     edgeNum[a]++;
     node *p=new node();
     p->to=b;
     p->w=w;
     vec[a].push_back(*p);
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int a,b,w;
         cin>>a>>b>>w;
         addEdge(a,b,w);
         addEdge(b,a,w);
     }
 }

 void dijkstra(int start){
     memset(dis,0x3f,sizeof(dis));
     dis[start]=;
     for(int i=;i<edgeNum[start];i++) {
         int b=vec[start][i].to;
         int w=vec[start][i].w;
         dis[b]=w;
     }
     vis[start]=;
     for(int k=;k<=n-;k++){
         int minV=0x7fffffff,min_i;
         for(int i=;i<=n;i++){
             if(!vis[i]&&dis[i]<minV){
                 minV=dis[i];
                 min_i=i;
             }
         }
         vis[min_i]=true;
         for(int i=;i<edgeNum[min_i];i++){
             int b=vec[min_i][i].to;
             int w=vec[min_i][i].w;
             if(!vis[b]&&dis[b]>dis[min_i]+w){
                 dis[b]=dis[min_i]+w;
             }
         } 

     }
 }

 //dijkstra的堆优化
 struct qnode{
     int i_i;
     int dis_i;
     qnode(int i,int dis_i){
         this->i_i=i;
         this->dis_i=dis_i;
     }
 };
 struct myCmp{
     bool operator ()(const qnode &p1,const qnode &p2){
         return p1.dis_i>p2.dis_i;
     }
 };
 priority_queue<qnode,vector<qnode>,myCmp> q;
 void dijkstra_2(int start){
     memset(dis,0x3f,sizeof(dis));//和SPFA一样，这里最开始全都是无穷大
     dis[start]=;
     q.push(qnode(start,dis[start]));
     while(!q.empty()){
         qnode p=q.top();
         q.pop();
         int min_i= p.i_i;
         int minV=p.dis_i;
         if(vis[min_i]) continue;
         vis[min_i]=true;
         for(int i=;i<edgeNum[min_i];i++){
             int b=vec[min_i][i].to;
             int w=vec[min_i][i].w;
             if(!vis[b]&&dis[b]>dis[min_i]+w){
                 dis[b]=dis[min_i]+w;
                 q.push(qnode(b,dis[b]));
             }
         }

     }
 } 

 void print(){
     for(int i=;i<=n;i++)
         cout<<dis[i]<<" ";
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     //dijkstra(2);
     dijkstra_2();
     print();
     return ;
 } 

关于上面的代码说几点：

1、堆优化的话priority_queue得非常熟悉

2、这里堆优化的时候使用了结构体，里面的成员是i和dis[i]，其实这个dis[i]可以直接写在外面，但是比较规则还是得自己定义

3、用队列做的所有的题核心代码一定是while(!queue.empty()){}

4、还是要多写多练，要熟悉，基础打好

5、和SPFA一样，如果点更新成功就加进队列

求节点1到其它节点的距离：

堆优化2

 #include <bits/stdc++.h>
 using namespace std;
 int n,m;
 struct node{
     int to;
     int w;
 };
 int edgeNum[];
 vector<node> vec[];
 int dis[];
 bool vis[];

 void addEdge(int a,int b,int w){
     edgeNum[a]++;
     node *p=new node();
     p->to=b;
     p->w=w;
     vec[a].push_back(*p);
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int a,b,w;
         cin>>a>>b>>w;
         addEdge(a,b,w);
         addEdge(b,a,w);
     }
 }

 void dijkstra(int start){
     memset(dis,0x3f,sizeof(dis));
     dis[start]=;
     for(int i=;i<edgeNum[start];i++) {
         int b=vec[start][i].to;
         int w=vec[start][i].w;
         dis[b]=w;
     }
     vis[start]=;
     for(int k=;k<=n-;k++){
         int minV=0x7fffffff,min_i;
         for(int i=;i<=n;i++){
             if(!vis[i]&&dis[i]<minV){
                 minV=dis[i];
                 min_i=i;
             }
         }
         vis[min_i]=true;
         for(int i=;i<edgeNum[min_i];i++){
             int b=vec[min_i][i].to;
             int w=vec[min_i][i].w;
             if(!vis[b]&&dis[b]>dis[min_i]+w){
                 dis[b]=dis[min_i]+w;
             }
         } 

     }
 }

 //dijkstra的堆优化
 struct myCmp{
     bool operator ()(int a,int b){
         return dis[a]>dis[b];
     }
 };
 priority_queue<int,vector<int>,myCmp> q;
 void dijkstra_2(int start){
     memset(dis,0x3f,sizeof(dis));//和SPFA一样，这里最开始全都是无穷大
     dis[start]=;
     q.push(start);
     while(!q.empty()){
         int u=q.top();
         q.pop();
         if(vis[u]) continue;
         vis[u]=true;
         for(int i=;i<edgeNum[u];i++){
             int b=vec[u][i].to;
             int w=vec[u][i].w;
             if(!vis[b]&&dis[b]>dis[u]+w){
                 dis[b]=dis[u]+w;
                 q.push(b);
             }
         }

     }
 } 

 void print(){
     for(int i=;i<=n;i++)
         cout<<dis[i]<<" ";
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     //dijkstra(2);
     dijkstra_2();
     print();
     return ;
 } 

堆优化2

关于上面的代码说几点：

1、dijkstra的优先队列优化写法和spfa非常像，只不过spfa多加了一个是否在队列里面的标志

2、这里储存图用的是vector数组

3、优先队列里面的元素是int，然而我们还是重写了优先队列的比较函数，因为队列里面是节点编号，但是我们要比较的是dis[i]

4、和SPFA一样，dis[i]最开始全都是无穷大 ,并且最开始只更新dis[start]=0

求节点1到其它节点的距离：

其它代码：

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int n,m,S,tot,Next[],head[],tree[],val[];
bool visit[];
long long dis[];
struct cmp
{
    bool operator()(int a,int b)
    {
        return dis[a]>dis[b];
    }
};
priority_queue<int,vector<int>,cmp> Q;
void add(int x,int y,int z)
{
    tot++;
    Next[tot]=head[x];
    head[x]=tot;
    tree[tot]=y;
    val[tot]=z;
}
int main()
{
    scanf("%d%d%d",&n,&m,&S);
    tot=;
    for (int i=;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        if (x==y) continue;
        add(x,y,z);
    }
    for (int i=;i<=n;i++)
    {
        visit[i]=false;
        dis[i]=;
    }
    Q.push(S);
    dis[S]=;
    while (!Q.empty())
    {
        int u=Q.top();
        Q.pop();
        if (visit[u]) continue;
        visit[u]=true;
        for (int i=head[u];i;i=Next[i])
        {
            int v=tree[i];
            if (!visit[v]&&dis[v]>dis[u]+(long long)val[i])
            {
                dis[v]=dis[u]+val[i];
                Q.push(v);
            }
        }
    }
    for (int i=;i<=n-;i++) printf("%lld ",dis[i]);
    printf("%lld\n",dis[n]);
    return ;
}

vector数组版

 #include <bits/stdc++.h>
 using namespace std;
 struct node{
     int v;
     int w;
     node(int v,int w){
         this->v=v;
         this->w=w;
     }
 };
 vector<node> vec[];
 int edgeNum[];
 int n,m;
 int dis[];
 bool vis[];

 void addEdge(int u,int v,int w){
     edgeNum[u]++;
     vec[u].push_back(node(v,w));
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         addEdge(u,v,w);
         addEdge(v,u,w);
     }
 }

 struct myCmp{
     bool operator ()(const int &u,const int &v){
         return dis[u]>dis[v];
     }
 };
 priority_queue<int,vector<int>,myCmp> q;
 void dijkstra(int start){
     memset(dis,0x3f,sizeof(dis));
     q.push(start);
     dis[start]=;
     while(!q.empty()){
         int u=q.top();
         q.pop();
         if(vis[u]) continue;
         vis[u]=true;
         for(int i=;i<edgeNum[u];i++){
             int v=vec[u][i].v;
             int w=vec[u][i].w;
             if(!vis[v]&&dis[v]>dis[u]+w){
                 dis[v]=dis[u]+w;
                 q.push(v);
             }
         }
     }
 }

 void print(){
     for(int i=;i<=n;i++){
         cout<<dis[i]<<" ";
     }
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     dijkstra();
     print();
     return ;
 }