6.3 基于二分搜索树、链表的实现的集合Set复杂度分析

两种集合类的复杂度分析

在【6.1】节与【6.2】节中分别以二分搜索树和链表作为底层实现了集合Set，在本节就两种集合类的复杂度分析进行分析：
测试内容：6.1节与6.2节中使用的书籍。
测试方法：测试两种集合类查找单词所用的时间

 //创建一个测试方法 Set<String> set:他们可以是实现了该接口的LinkedListSet和BSTSet对象
    private static double testSet(Set<String> set, String filename) {
        //计算开始时间
        long startTime = System.nanoTime();
        System.out.println("Pride and Prejudice");
        //新建一个ArrayList存放单词
        ArrayList<String> words1 = new ArrayList<>();
        //通过这个方法将书中所以单词存入word1中
        FileOperation.readFile(filename, words1);
        System.out.println("Total words : " + words1.size());

        //增强for循环，定一个字符串word去遍历words
        //底层的话会把ArrayList words1中的值一个一个的赋值给word
        for (String word : words1)
            set.add(word);//不添加重复元素
        System.out.println("Total  different words : " + set.getSize());

        //计算结束时间
        long endTime = System.nanoTime();
        return (endTime - startTime) / 1000000000.0;//纳秒为单位
    }

    public static void main(String[] args) {
        //基于二分搜索的集合
        BSTSet<String> bstSet = new BSTSet<>();
        double time1 = testSet(bstSet, "pride-and-prejudice.txt");
        System.out.println("BSTSet:" + time1 + "s");
        System.out.println("————————————————————");
        //基于链表实现的集合
        LinkedListSet<String> linkedListSet = new LinkedListSet<>();
        double time2 = testSet(linkedListSet, "pride-and-prejudice.txt");
        System.out.println("linkedListSet:" + time2 + "s");

    }

结果：BSTSet的速度比LinkedListed的速度快

集合的时间复杂度分析：

1.链表情况

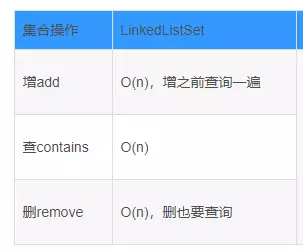
2.二叉搜索树的情况

在基于二叉搜索树的情况下，增加、查询、删除的与二叉搜索树的深度有关，每次操作均为从根节点到某一一支子树的叶子节点之间进行操作，时间复杂度为0(h),h表示二叉搜索树的高度（层数）。

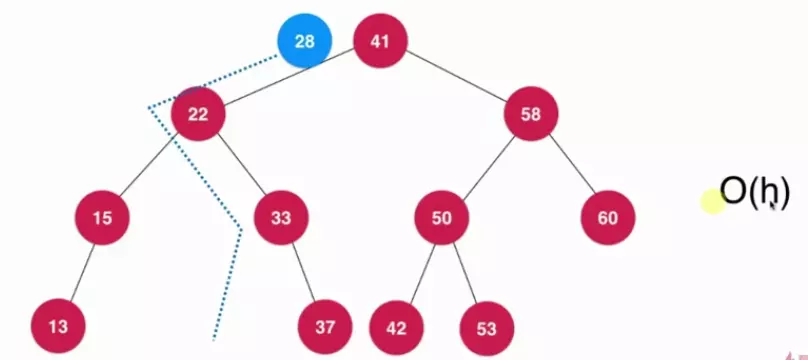
二叉搜索树复杂度如下：

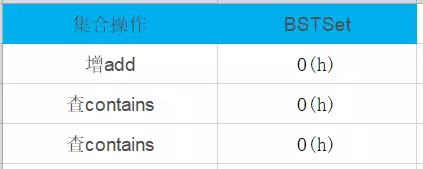
2.1 探究链表情况下的n与二叉搜索树的h的关系

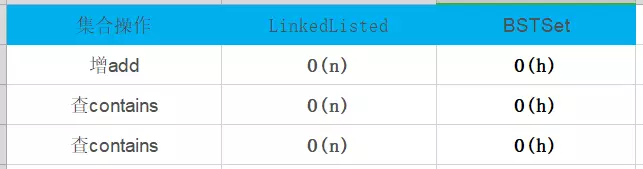
下面对n与h关系进行推导：

2.1.1 采用满二叉树的情况进行分析（最优情况）

采用满二叉树（每个节点都有左右节点，除了叶子节点）来进行分析的原因为满二叉树是一种极端情况，如下图：

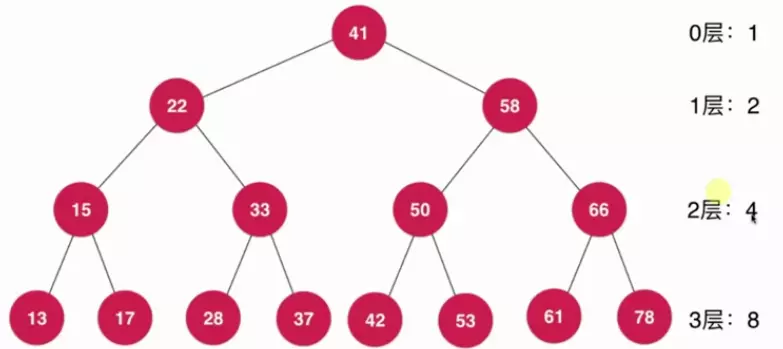
从上图中关于h层总共有多少个节点有如下推导：

假设节点个数为n个则有如下关系：

针对都是log级别的关系，底数是多少不影响它是log级别的则有：

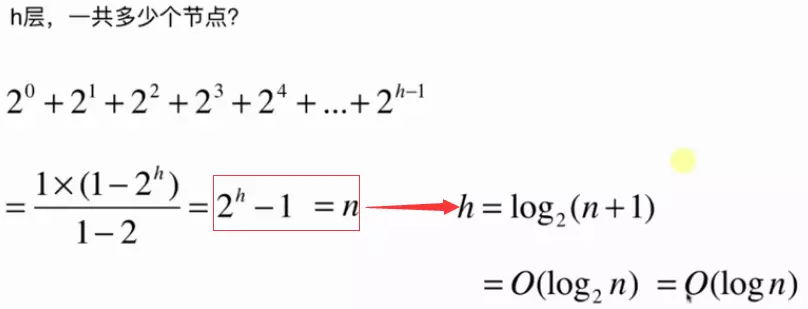
2.1.2 单个孩子情况----二叉搜索树最坏情况（节点数等于其高度）

比如：下面这种二叉搜索树

对于这种只有单个孩子的情况，此时二叉搜索树退化成了链表，此时的时间复杂度为O(n)。

2.2 两种集合复杂度统计

2.2.1 logn和n的差距

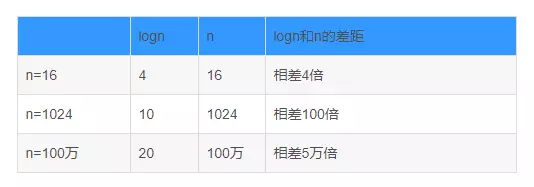
推荐是最好的支持，关注是最大的鼓励。亲爱的朋友，很荣幸在园子里遇到您。

本节涉及的源码地址为   https://github.com/FelixBin/dataStructure/tree/master/src/SetPart