[matlab] 8.蚁群算法解决TSP问题

城市坐标数据下载  密码：07d5

求遍历这52座城市后最后回到最初城市的最短距离

%% 第9章 蚁群算法及MATLAB实现——TSP问题
% 程序9-1

%% 数据准备
% 清空环境变量
clear all
clc

% 程序运行计时开始
t0 = clock;

% 导入数据
citys = xlsread('berlin52.xlsx','B2:C53');

%% 计算城市间距离
n = size(citys,1); %城市数
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum( ( citys(i,:) - citys(j,:) ).^2 ) ); %两点之间的距离
        else
            D(i,j) = 1e-4;          %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值
        end
    end
end

%% 初始化参数
m = 40;                     % 蚂蚁数量最好接近城市数量的1.5倍
alpha = 1;                  % 信息素重要程度因子[1,4]最好
beta = 5;                   % 启发函数重要程度因子 5最好
vol = 0.2;                  % 信息素挥发(volatilization)因子
Q = 10;                     % 常系数
Heu_F = 1./D;               % 启发函数(heuristic function)
Tau = ones(n,n);            % 信息素矩阵
Table = zeros(n,n);         % 路径记录表
iter = 1;                   % 迭代次数初值
iter_max = 500;             % 最大迭代次数 [100,500]
Route_best = zeros(iter_max,n);     % 各代最佳路径
Length_best = zeros(iter_max,1);    % 各代最佳路径的长度
Length_ave = zeros(iter_max,1);     % 各代路径的平均长度
Limit_iter = 0;                     % 程序收敛时迭代次数

%% 迭代寻找最佳路径
while iter <= iter_max
    % 随机产生各个蚂蚁的起点城市
    start = zeros(m,1);
    for i = 1:m
        temp = randperm(n); %randperm函数打乱顺序 1-n随机排序
        start = temp(1);
    end
    Table(:,1) = start; %路径记录表
    % 构建解空间
    citys_index = 1:n;
    % 逐个蚂蚁路径选择
    for i =1:m
        % 逐个城市路径选择
        for j = 2:n
            tabu = Table(i,1:(j - 1));                  % 已访问的城市集合（禁忌表）
            allow_index = ~ismember(citys_index,tabu);  % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵；
            allow = citys_index(allow_index);           % 待访问的城市集合
            P = allow;
            % 计算城市间转移概率
            for k = 1:length(allow)
                P(k) = Tau(tabu(end),allow(k))^alpha *  Heu_F(tabu(end),allow(k))^beta;  %线路选择概率的分子
            end
            P = P / sum(P); %线路选择概率的分母
            % 轮盘赌法选择下一个访问城市
            Pc = cumsum(P);             %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15]
            target_index = find(Pc >= rand);
            target = allow(target_index(1));
            Table(i,j) = target;
        end
    end
    % 计算各个蚂蚁的路径距离
    Length = zeros(m,1);
    for i = 1:m
        Route = Table(i,:);
        for j = 1:(n - 1)
            Length(i) = Length(i) + D(Route(j),Route(j + 1));
        end
        Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点
    end
    % 计算最短路径距离及平均距离
    if iter == 1
        [min_Length, min_index] = min(Length);
        Length_best(iter) = min_Length;
        Length_ave(iter) = mean(Length);
        Route_best(iter,:) = Table(min_index,:);
        Limit_iter = 1;
    else
        [min_Length,min_index] = min(Length);
        Length_best(iter) = min(Length_best(iter - 1),min_Length);
        Length_ave(iter) = mean(Length);
        if Length_best(iter) == min_Length
            Route_best(iter,:) = Table(min_index,:);
            Limit_iter = iter;
        else
            Route_best(iter,:) = Route_best((iter - 1),:);
        end
    end
    % 更新信息素
    Delta_Tau = zeros(n,n); %信息素增量
    % 逐个蚂蚁计算
    for i = 1:m
        % 逐个城市计算
        for j = 1:(n - 1)
            Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数
        end
        Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值
    end
    Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量
    % 迭代次数加1,清空路径记录表
    iter = iter + 1;
    Table = zeros(m,n);
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
Time_Cost = etime(clock,t0);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]);
disp(['收敛迭代次数:' num2str(Limit_iter)]);
disp(['程序执行时间:' num2str(Time_Cost),'秒']);

%% 绘图
set(gca,'LineWidth',1.5); %边框加粗,美观
figure(1)
%  假设各个城市的X坐标为zuobiao_X，Y坐标为zuobiao_Y，zuobiao_X(i)表示第i个城市的横坐标，一共有n个城市，那么，采用以下循环语句进行画图：
%  for i=1:n-1
%  plot([zuobiao_X(i),zuobiao_X(i+1)],[zuobiao_Y(i),zuobiao_Y(i+1)],'-r');
%  hold on;
%  end
plot([ citys(Shortest_Route,1);citys(Shortest_Route(1),1) ], [ citys(Shortest_Route,2);citys(Shortest_Route(1),2) ], 'k.-','Markersize',20);
set(gca,'LineWidth',1.5); %边框加粗,美观
grid on;
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['  ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'    起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'    终点')
xlabel('城市位置横坐标');
ylabel('城市位置纵坐标');
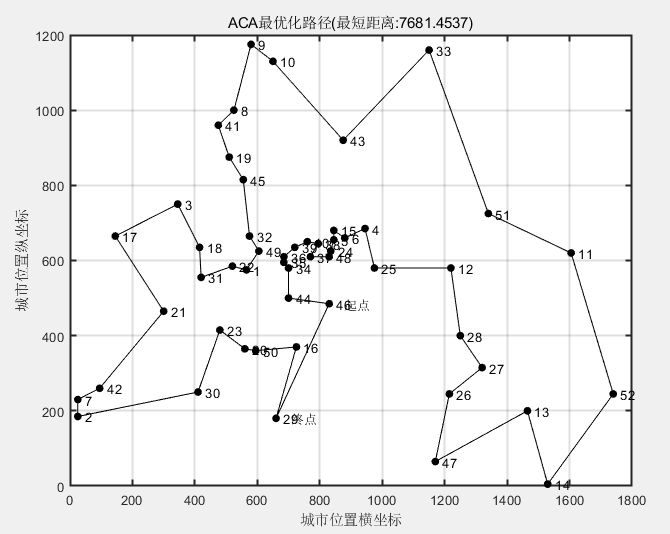
title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']);
figure(2);
plot(1:iter_max,Length_best,'b');
set(gca,'LineWidth',1.5); %边框加粗,美观
legend('最短距离');
xlabel('迭代次数');
ylabel('距离');
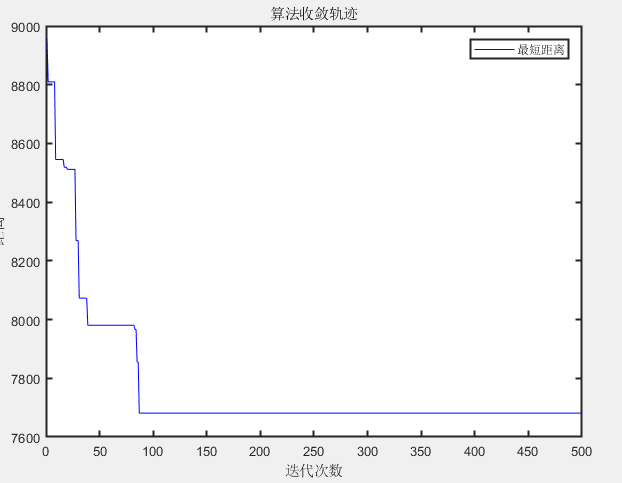
title('算法收敛轨迹');
set(gca,'LineWidth',1.5);  %边框加粗,美观
 

蚁群算法

最短距离:7681.4537
最短路径:46 44 34 35 36 39 40 38 37 48 24 5 15 6 4 25 12 28 27 26 47 13 14 52 11 51 33 43 10 9 8 41 19 45 32 49 1 22 31 18 3 17 21 42 7 2 30 23 20 50 16 29 46
收敛迭代次数:398
程序执行时间:38.67秒