【[USACO08JAN]haybale猜测Haybale Guessing】

抄题解.jpg

完全完全不会啊，这道题简直太神了

不过抄题解可真开心

首先这道题目保证了每一个位置上的数都是不同的，那么就能得到第一种判断不合法的方式

如果两个区间的最小值一样，但是两个区间的交集为空集，那么就是不合法的

因为最小值肯定来自于同一个位置

之后就是第二种情况

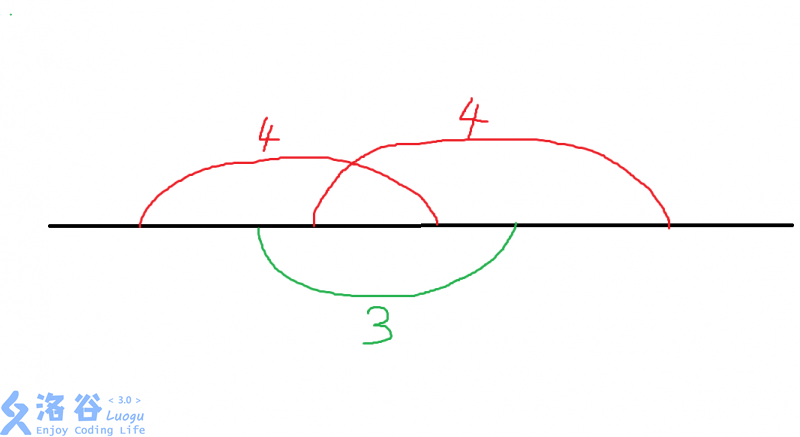
上面那两个红色区间的最小值是\(4\)，但是下面那个被完全包含的绿色区间的最小值是\(3\)这显然非常不合法

但是如果是这个样子呢

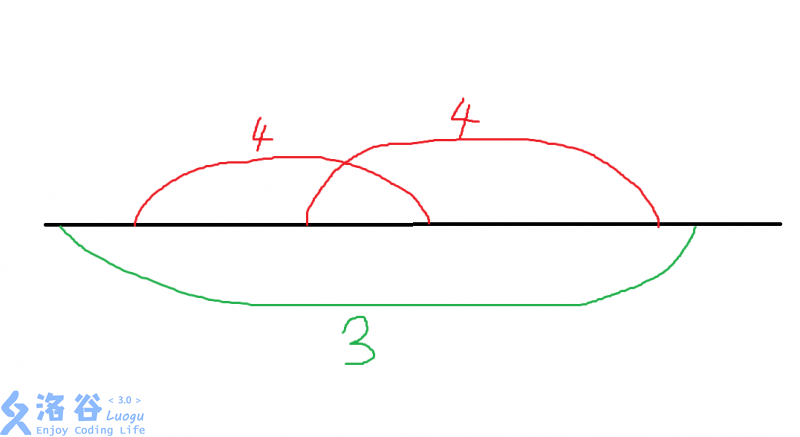
显然是可以的，因为那些\(3\)可以来自红色区间以外的位置

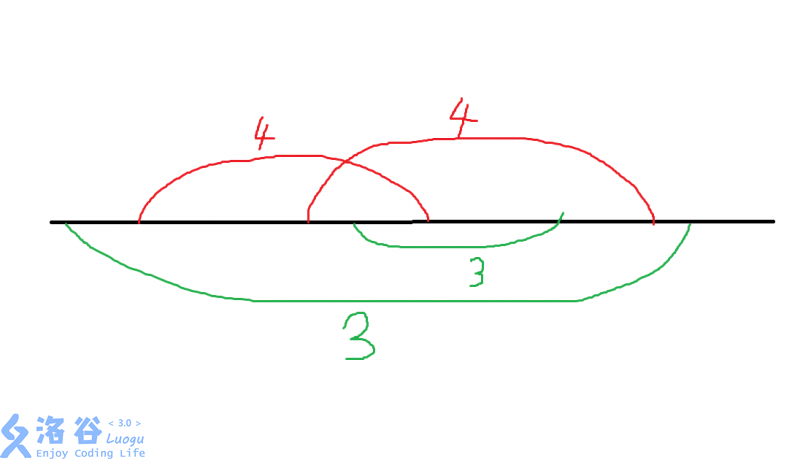
就有不行了，因为这个时候\(3\)又只能来自于那个较小的绿色区间了，而那个较小的绿色区间又被红色完全覆盖了

这个时候就能得出第二个判断方法

如果最小值相同的区间，其交集被最小值比它的区间的并集覆盖，那么就不合法

所以我们需要覆盖并集，判断交集是否被完全覆盖

显然区间的交集和并集随手就能求出来，但是覆盖这个问题得需要一棵线段树来判断

同时为了方便的进行判断\(2\)，我们得让区间的最小值是有序的，所以一个一个扫是行不通了，我们得二分答案，找到最后一个合法的位置\(+1\)就是答案了

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define LL long long
#define re register
#define maxn 25005
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
struct Seg
{
	int x,y,q;
}a[maxn],b[maxn];
int l[4000005],r[4000005],d[4000005],tag[4000005];
int n,m;
inline int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9')
		x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x;
}
void build(int x,int y,int i)
{
	l[i]=x,r[i]=y;
	if(x==y) return;
	int mid=x+y>>1;
	build(x,mid,i<<1),build(mid+1,y,i<<1|1);
}
void clear(int x,int y,int i)
{
	d[i]=0,tag[i]=0;
	if(x==y) return;
	int mid=x+y>>1;
	clear(x,mid,i<<1),clear(mid+1,y,i<<1|1);
}
inline void pushdown(int i)
{
	if(!tag[i]) return;
	tag[i<<1]=tag[i<<1|1]=1;
	d[i<<1]=r[i<<1]-l[i<<1]+1;
	d[i<<1|1]=r[i<<1|1]-l[i<<1|1]+1;
	tag[i]=0;
}
void change(int x,int y,int i)
{
	if(x<=l[i]&&y>=r[i])
	{
		d[i]=r[i]-l[i]+1;
		tag[i]=1;
		return;
	}
	pushdown(i);
	int mid=l[i]+r[i]>>1;
	if(y<=mid) change(x,y,i<<1);
		else if(x>mid) change(x,y,i<<1|1);
			else change(x,y,i<<1|1),change(x,y,i<<1);
	d[i]=d[i<<1]+d[i<<1|1];
}
int query(int x,int y,int i)
{
	if(x<=l[i]&&y>=r[i]) return d[i];
	pushdown(i);
	int mid=l[i]+r[i]>>1;
	if(y<=mid) return query(x,y,i<<1);
	if(x>mid) return query(x,y,i<<1|1);
	return query(x,y,i<<1)+query(x,y,i<<1|1);
}
inline int cmp(Seg A,Seg B)
{
	return A.q>B.q;
}
inline int check(int now)
{
	for(re int i=1;i<=now;i++)
		b[i]=a[i];
	std::sort(b+1,b+now+1,cmp);
	clear(1,n,1);
	int pre=1,nl=b[1].x,nr=b[1].y,Ul=b[1].x,Ur=b[1].y;
	for(re int i=2;i<=now;i++)
	{
		if(b[i].q==b[pre].q)
		{
			nl=max(nl,b[i].x);
			Ul=min(Ul,b[i].x);
			Ur=max(Ur,b[i].y);
			nr=min(nr,b[i].y);
		}
		else
		{
			if(nl>nr) return 0;
			if(query(nl,nr,1)==nr-nl+1) return 0;
			change(Ul,Ur,1);
			pre=i;
			nl=Ul=b[i].x,nr=Ur=b[i].y;
		}
	}
	if(nl>nr) return 0;
	if(query(nl,nr,1)==nr-nl+1) return 0;
	return 1;
}
int main()
{
	n=read(),m=read();
	for(re int i=1;i<=m;i++) a[i].x=read(),a[i].y=read(),a[i].q=read();
	build(1,n,1);
	int L=1,R=m;
	int ans=0;
	while(L<=R)
	{
		int mid=L+R>>1;
		if(check(mid)) L=mid+1,ans=mid;
			else R=mid-1;
	}
	if(ans==m) puts("0");
		else printf("%d\n",ans+1);
	return 0;
}