[学习笔记]搜索——模拟与dp的结合

搜索：

一种基础的算法。

考察常见于NOIP

但是高级的搜索算法可能还会在省选出现。

50%以上的暴力都可以用搜索直接枚举来写。

但是，当数据规模不是很大的时候，搜索也可能成为正解。

（比如剪枝PK状压dp）

在搜索的基础上，可以衍生出最短路，而dp本质上，也是搜索的剪枝。

一、基础搜索算法

DFS：

最基本的搜索。用递归实现。

顾名思义，深度优先搜索的特点就是从一个位置直接搜下去，直到搜到末尾或者中途return

先扩展出深度。

dfs图中遍历的状态会形成一棵搜索树。（如果搜成了一般图，那就说明剪枝不到位了）

一般认为，dfs的复杂度就是“搜索树的大小 乘上 每一个状态 下的复杂度”

搜索的优点：可以不用记录状态。开一个全局变量即可。所有的函数也可以围绕这个变量展开。

自我感觉，dfs的更多时候，用途不在于搜索，而在于对结构的遍历。

用途：

1.50%的暴力，2^n,n!的枚举。

2.容斥。

3.遍历。

dfs遍历一棵树（可能爆栈），（求dfs序，树形dp等）

因为dfs会搜完一棵子树再回溯，所以利用这个性质，dfn，dfn2，以及tarjan都可以成立。

利用递归的性质，从儿子回溯后，对这一层的检查与更新，也是经常用到的。

4.配合BFS，寻找联通块

BFS：

最基本的遍历图的方法。一般用于搜索。

顾名思义，广度优先搜索，就是先扩展整个图的层数。

会从一个起点（多个起点）开始，不断把周围一层遍历，

即，遍历的状态的层数总是连续的一段。

用途：

1.边权为1的最短路。

这个其实是值得注意的，BFS的最短路是O(n+m)的，是所有的最短路中最快的。（有时那SPFA或者dij跑边权为1的最短路，就浪费了~~~）

当然，必须边权是1。

2.分层图：
利用BFS的分层图的性质，可以有层次地遍历一个结构。

AC自动机的fail树的构建：由于分层图，而fail[i]一定长度比i小，即层的编号小，所以必然已经遍历，没有后效性。

DINIC算法，在分层图上跑增广路。可以保证复杂度。

问题：

1.DFS的劣势明显，会进入一个搜索子树，遍历完这棵搜索树之后才会回溯。

如果这棵搜索树对答案不能产生影响，那么会大大降低效率。

更糟糕的，如果一棵子树非常庞大（指数级增长），则直接TLE地飞起。

2.BFS的劣势明显，由于要广度优先搜索，所以会遍历完整个一层才会遍历下一层。

如果一层很多，也会爆炸。

而且，必须记录所有当前在队列里状态的状态信息。

如果状态增多，搜索树较大，空间和时间都没有办法保证。

对于这些bug，机智的人们创建了新的优化方法。

二、剪枝

剪枝，顾名思义，就是在dfs或者bfs中，把一棵搜索子树直接砍去，不进行遍历。

来达到复杂度的保证。

其实剪枝范围可以很广，A*，IDA*，甚至dp，我认为都可以叫剪枝。

而且剪枝也不一定用于搜索。

当然，一般情况下的剪枝，就是指用dfs搜索中的剪枝。

1.最优性剪枝。

最常见。最基本的，对于单增取min，单减取max，都可以稳定减去一些复杂度。

配合估价函数，IDA*，对未来最少花费进行预估，通常可以大大增加效率。

2.可行性剪枝。

对于状态搜索下去是否能合法的剪枝。

3.预处理。

这个是经常忘记的，但是非常有用的“剪枝”

因为，通常搜索题的规模不大，扫一遍地图预处理根本不是瓶颈。

而由于搜索过程中，同一个位置可能遍历多次。每次再找合法的解，就很慢了。

经典例题BFS预处理：华容道

剪枝最重要的还是分析题目的性质。

剪枝能提前判断就提前判断。

例题：NOIP2004 虫食算

Mayan游戏

生日蛋糕

三、搜索进阶

其实都是剪枝。

A*，IDA*，迭代加深复杂度都是玄学。

和经验、人品、数据湿度成正比。

1.折半爆搜

dfs。举例，n大概在40左右，可以2^(n/2)爆搜。存储状态，然后可以合并。

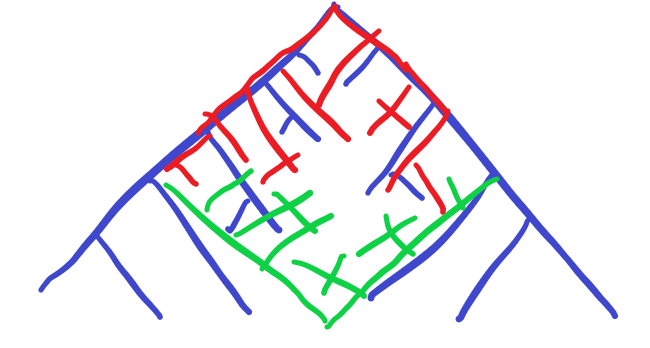
蓝色是一般的正向搜索，两边dfs是红色和绿色部分。可以节省很多分支。

难点：状态存储和合并。

存储：数组，大了用map

合并：在dfs2到头的时候合并，或者可以搜完之后把状态sort，然后双指针等等。

例题：POJ1186 折半爆搜+双指针

2.双向广搜

bfs。对于走迷宫等状态可逆的题目类型

bfs1走一层，bfs2走一层，循环往复，直到在bfs1中碰到bfs2走过的路径或者反之，就可以停止。

通常适用于有固定起点和终点的。

通常使用哈希表存储经过路径。

例题：万圣节后的早晨&&九数码游戏——双向广搜

3.A*

思想：和BFS结合，设计一个估价函数。对未来的最小步数进行估价，估价函数h(S)，实际代价g(S)。

每次选择g(S)+h(S)最小的进行扩展

第一次到达终点的就是最优解。

估价函数必须小于等于实际最小代价。否则可能会代替最优解，或者说，第一次到终点的不是最优解。

例题：
k短路，扩展一下，第k次到终点的就是第k短。

八数码，不同的位置数字个数作为估价。

4.迭代加深搜索。

有的时候，一个搜索树的增长非常迅速，子树非常庞大。

甚至子树是无穷大的。。。。

dfs会陷入其中无法自拔。

那么，如果问题答案步数不会很多（15步以内），甚至有提示：x步以内无解则-1

很可能就是迭代加深搜索。

有什么用？

限制搜索的深度，使得dfs在到达深度的时候，就会回溯。

重复搜索？

是的。但是比起庞大的树来说，不算什么。

5.IDA*

说是A*，但是主要是A*估价函数的思想。

因为是dfs，并没有像A*一样每次拓展最小的。

说白了，就是在迭代加深的dfs中，在剪枝里加入对未来步数的估价，

限制是：当前深度+预估步数>迭代上限，return

由于当前深度不会太深，所以可以很快判断return

传说非常好用。

例题：埃及分数&&The Rotation Game&&骑士精神——IDA*

四、正确性玄学算法

略。