t检验&z检验学习[转载]

转自:https://blog.csdn.net/m0_37777649/article/details/74937242

1.什么是T检验？

T检验是假设检验的一种，又叫student t检验（Student’s t test），主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布资料。 
T检验用于检验两个总体的均值差异是否显著。

2.单总体t检验例子

“超级引擎”工厂是一家专门生产汽车引擎的工厂，根据政府发布的新排放要求，引擎排放平均值应低于20ppm，如何证明生产的引擎是否达标呢？（排放量的均值小于20ppm）

2.1思路1

一个直接的想法就是，把这个工厂所有的引擎都测试一下，然后求一下排放平均值就好了。比如工厂生产了10个引擎，排放水平如下：
15.6 16.2 22.5 20.5 16.4
19.4 16.6 17.9 12.7 13.9
排放平均值为
(15.6+16.2+22.5+20.5+16.4+19.4+16.6+17.9+12.7+13.9)/10=17.17(15.6+16.2+22.5+20.5+16.4+19.4+16.6+17.9+12.7+13.9)/10=17.17
小于政府规定的20ppm，合格！

这也太简单了！

然而，随着“超级引擎”工厂规模逐渐增大，每天可以生产出10万个引擎，如果把每个引擎都测试一遍，估计要累死人了……
有没有更好的方法？

2.2思路2

由于引擎数量太多，把所有引擎测试一遍太麻烦了，一个好想法：
可不可以采用“反证法”？先假设所有引擎排放量的均值为μμ，然后随机抽取10个引擎，看看这10个引擎的排放量均值与假设是否相符，如果相符，则认为假设是正确的，反之认为假设是错误的。这样，就可以通过一小部分数据推测数据的总体.

具体怎么操作呢？

先建立两个假设，分别为:
H0:μ⩾20 (原假设)
H1:μ<20 (备择假设)
【μ代表总体(所有引擎的排放量)均值】

在原假设成立的基础上，求出”取得样本均值或者更极端的均值”的概率，如果概率很大，就倾向于认为原假设H0是正确的，如果概率很小，就倾向于认为原假设H0是错误的，从而接受备择假设H1。

那么如何求这个概率p呢？
这就需要引入一个概念——统计量
简单的讲，统计量就类似于用样本已知的信息(如样本均值，样本标准差)构建的一个“标准得分”，这个“标准得分”可以让我们求出概率p

由于样本服从正态分布，且样本数量较小(10)，所以这里要用到的统计量为t统计量，公式如下：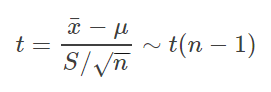

现在抽取出10台引擎供测试使用，每一台的排放水平如下： 
15.6 16.2 22.5 20.5 16.4 
19.4 16.6 17.9 12.7 13.9

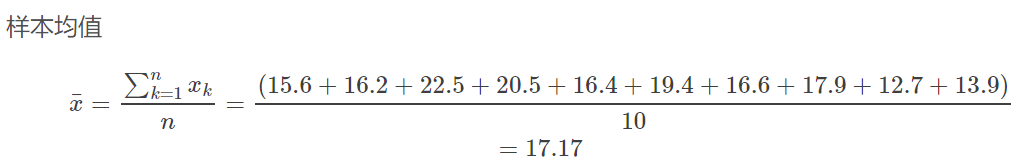
样本方差：

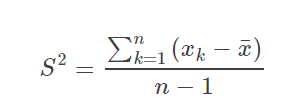
样本标准差:

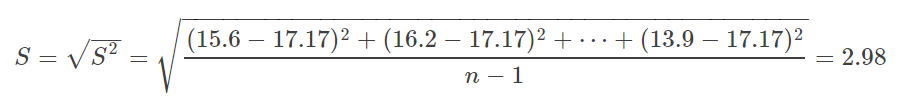
我们把原假设μ⩾20 拆分，先考虑μ=20μ=20的情况 
将数值带入t统计量公式中，可以得出

由于t统计量服从自由度为9的t分布，我们可以求出t统计量小于-3.00的概率，即下图阴影部分面积

2.3P值——检验结果讨论

通过查询t分位数表(见附录)，我们可知，当自由度为9时，t统计量小于-2.821的概率为1%，而我们求得的t统计量为-3.00，所以t统计量小于-3.00的概率比1%还要小(因为-3.00在-2.81的左边，所以阴影面积更小)。
这个概率值通常被称作“p值”，即在原假设成立的前提下，取得“像样本这样，或比样本更加极端的数据”的概率。

3.第一类错误与第二类错误

在例1中，我们认为1%的概率很小，所以更倾向于认为原假设是错误的，从而接受了备择假设。但这样的判断是准确的吗？为了探讨这个问题，我们考虑以下四种情况：

4.α值——T检验标准流程

α值通常取0.05 0.01 0.1等，用来确定t值的拒绝域，拒绝域的意思是拒绝原假设H0.

所以利用t检验做出的结论并不是百分之百正确的，仍有很小的几率会犯错误。对于上面的例子，有些人会认为1%的概率已经很小了，可以拒绝原假设，还有些人会认为1%的概率虽然很小，但不足以拒绝原假设。为了解决这个问题，统计学家们提出了一个阈值，如果犯第一类错误（拒真）的概率小于这个阈值，就认为可以拒绝原假设，否则认为不足以拒绝原假设。这个阈值就叫α。

5.假设形式与拒绝域

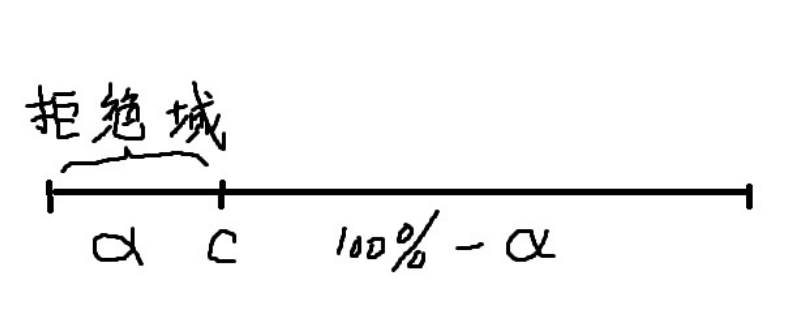
类别2称为单尾检验 
备择假设中包含>的情形，拒绝域在数轴右侧

备择假设中包含<的情形，拒绝域在数轴左侧

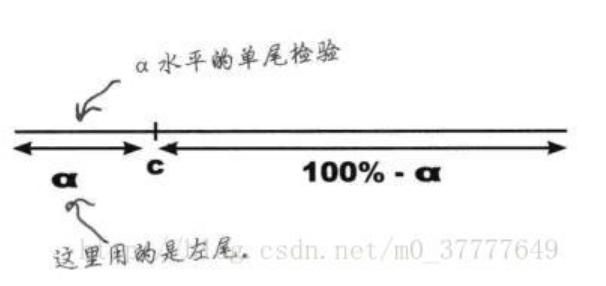
6.总结——T检验的种类

6.1单总体t检验

6.2双总体T检验

6.3配对样本t检验

7.z检验

转自：https://wenku.baidu.com/view/50d00d7d4b7302768e9951e79b89680203d86bc6.html

其中σ0是方差，s是标准差

例子：

那么这个P值是怎么找的呢?

转自:https://wenku.baidu.com/view/df02171ca76e58fafab003f9.html

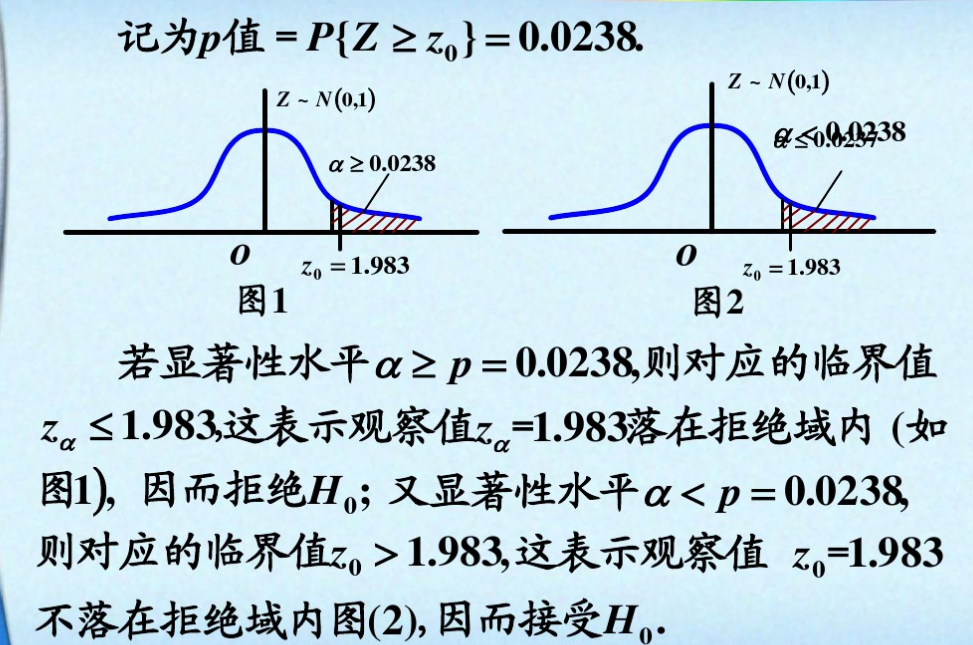
查正态分布Z值表即可。