【cs229-Lecture9】经验风险最小化

写在前面：机器学习的目标是从训练集中得到一个模型，使之能对测试集进行分类，这里，训练集和测试集都是分布D的样本。而我们会设定一个训练误差来表示测试集的拟合程度（训练误差），虽然训练误差具有一定的参考价值。但实际上，我们并不关心对训练集合的预测有多么准确。我们更关心的是对于我们之前没有见过的一个全新的测试集进行测试时，如果利用这个模型来判断，会表现出怎么样的性能，即一般误差。因此，这也要求我们的模型需要具备一定的泛化能力。泛化能力弱，就会出现欠拟合与过拟合的情况。

偏差/方差（Bias/variance）

1、欠拟合与过拟合

解决的问题就是：建立一个模型，对何时出现欠拟合与过拟合进行说明。

eg：线性分类问题

Logistic回归，简化版模型：

a、定义一个训练误差（经验风险）(training error，empirical risk ， empirical error）

含义：被假设错误分类的样本在训练样本中所占的比例=被假设错误分类的样本数之和/m

引出经验风险最小化（Empirical Risk Minization，ERM）

含义：取经验误差最小的参数

---

即证明ERM是一个合理的算法：能带来更小的一般误差

两条引理：联合界（Union bound）、一致收敛（Uniform Convergence）。

1、联合界（Union bound）和 Hoeffding不等式

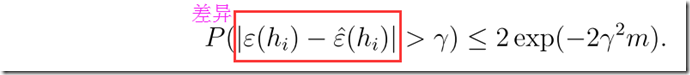
含义：Hoeffding不等式说的是估值的差异有一个上界，即给定一个假设，训练误差会以一个很大的概率接近于一般误差

---

最终想证明的是，对于整个假设类而言，训练误差对于一般误差是一个很好的估计，而不仅仅只是对某一个假设成立。

一致（当m很大时，训练误差接近与一般误差）收敛

给定多大的m，才能是的一般误差和训练误差近似呢？