Kruskal算法求最小生成树

Kruskal算法是根据权来筛选节点，也是采用贪心算法。

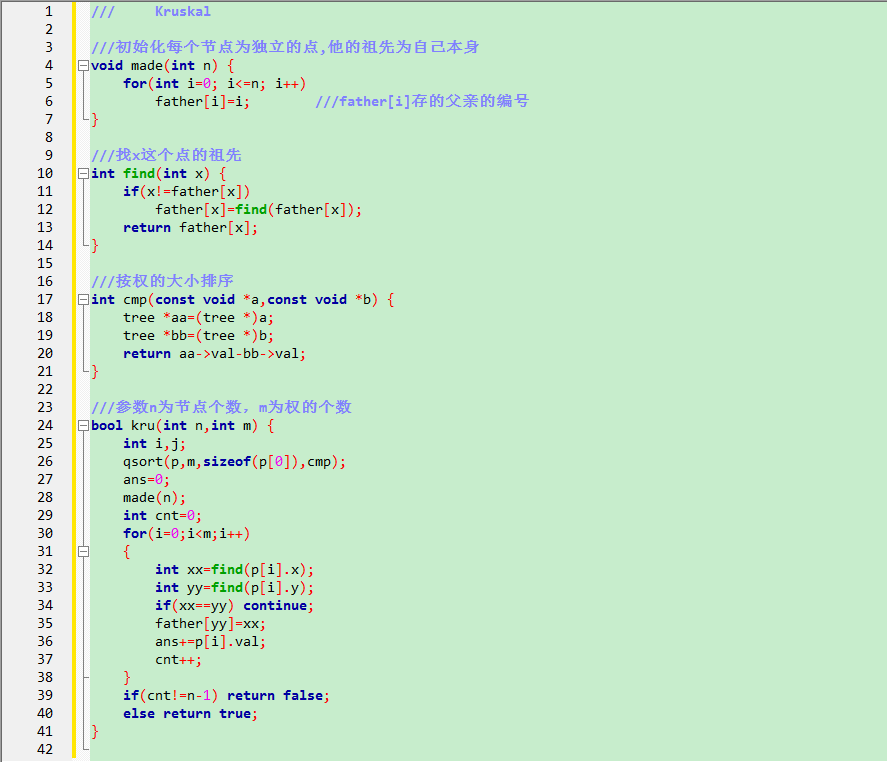
///     Kruskal

///初始化每个节点为独立的点,他的祖先为自己本身
void made(int n) {
    for(int i=; i<=n; i++)
        father[i]=i;        ///father[i]存的父亲的编号
}

///找x这个点的祖先
int find(int x) {
    if(x!=father[x])
        father[x]=find(father[x]);
    return father[x];
}

///按权的大小排序
int cmp(const void *a,const void *b) {
    tree *aa=(tree *)a;
    tree *bb=(tree *)b;
    return aa->val-bb->val;
}

///参数n为节点个数，m为权的个数
bool kru(int n,int m) {
    int i,j;
    qsort(p,m,sizeof(p[]),cmp);
    ans=;
    made(n);
    int cnt=;
    for(i=;i<m;i++)
    {
        int xx=find(p[i].x);
        int yy=find(p[i].y);
        if(xx==yy) continue;
        father[yy]=xx;
        ans+=p[i].val;
        cnt++;
    }
    if(cnt!=n-) return false;
    else return true;
}