洛谷P3374树状数组1

下有彩蛋（from https://www.cnblogs.com/wuwangchuxin0924/p/5921130.html）
树状数组的blog写的最好的是这位//https://www.cnblogs.com/wuwangchuxin0924/p/5921130.html//（声明一下跟我没有半毛钱关系，我是一个热爱珂学的好孩子）
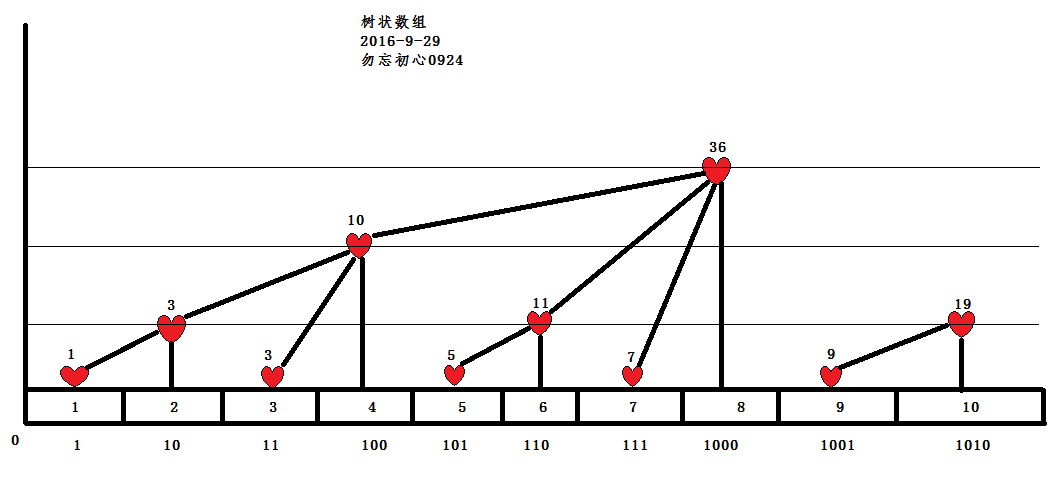
我要说的主要是怎么去学习树状数组，刚开始我也无从下手，但是我想到了一个方法，虽然我不知道怎么实现，但我知道代码的意思和实现的原理，所以我对照他（她）的代码在看着他（她）的图去思考，就懂了。
图就是这张↓

非常的清晰只要跟着代码走就好了，但我不喜欢他（她）的代码，所以给你们我的代码作为一个参考，你们也可以看他（她）的。

 #include<bits/stdc++.h>
 using namespace std;
 int n,m,a[],c[];
 int lowbit(int x){
     return x&(-x);//这个是求末尾零的个数的，因为只要末尾有零的都是2^n次方（n自己代）
 }
 void add_tree(int x,int y){//和线段树不一样这是一个一个数处理的
     while (x<=n){
         c[x]+=y;
         if (lowbit(x)==) return;//如果后面没有零了，有可能死循环
         x+=lowbit(x);//这个就是我说的要对着图看的，因为前面的数不可能再加给更前面的区间所以只要考虑给后面的加
     }
 }
 int sum(int x){//求出1到x区间的和，就是add_tree的逆过程
     int ans=;
     while (x>){
         ans+=c[x];
         if (lowbit(x)==) return ans;
         x-=lowbit(x);
     }
     return ans;
 }
 int main(){
      cin>>n>>m;
      for (int i=;i<=n;i++) cin>>a[i];
      for (int i=;i<=n;i++) add_tree(i,a[i]);
      for (int i=;i<=m;i++){
          int a,b,c;
          cin>>a>>b>>c;
          if (a==) add_tree(b,c);
          else cout<<sum(c)-sum(b-)<<endl;//因为b这个点也要加所以b-1
      }
 }

/*

                   _ooOoo_
                  o8888888o
                  88" . "88
                  (| -_- |)
                  O\  =  /O
               ____/`---'\____
             .'  \\|     |//  `.
            /  \\|||  :  |||//  \
           /  _||||| -:- |||||-  \
           |   | \\\  -  /// |   |
           | \_|  ''\---/''  |   |
           \  .-\__  `-`  ___/-. /
         ___`. .'  /--.--\  `. . __
      ."" '<  `.___\_<|>_/___.'  >'"".
     | | :  `- \`.;`\ _ /`;.`/ - ` : | |
     \  \ `-.   \_ __\ /__ _/   .-` /  /
======`-.____`-.___\_____/___.-`____.-'======
                   `=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
         I have a dream!A AC deram!!
 orz orz orz orz orz orz orz orz orz orz orz
 orz orz orz orz orz orz orz orz orz orz orz
 orz orz orz orz orz orz orz orz orz orz orz

*/
这个好

致所以OIer（from https://www.cnblogs.com/wuwangchuxin0924/p/5921130.html）（从不侵权的小宝宝）