【bzoj3122】: [Sdoi2013]随机数生成器 数论-BSGS

【bzoj3122】: [Sdoi2013]随机数生成器

当a>=2 化简得

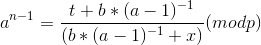
然后 BSGS 求解

其他的特判 ：

当 x=t  n=1

当 a=1 

当 a=0 判断b==t

 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <map>
 #include <algorithm>
 using namespace std;

 #define LL long long
 int T;
 LL a,b,x,t,p;

 LL Q_pow(LL x,LL y,LL p){
     LL ans=;
     while (y){
         if (y&) ans=ans*x%p;
         x=x*x%p; y=(y>>);
     }
     return ans;
 }

 LL BSGS(LL a,LL b,LL p){
     if ((a== && b!=) || (a== && b!=)) return -;
     map<LL,LL> x;
     LL sz=ceil(sqrt(p)),k=,inv;
     x.clear();
     x[]=; inv=Q_pow(Q_pow(a,sz,p),p-,p);
     for (int i=;i<sz;i++){
         k=k*a%p;
         if (!x.count(k)) x[k]=i;
     }
     for (int i=;i<sz;i++){
         if (x.count(b)) return i*sz+x[b];
         b=b*inv%p;
     }
     return -;
 }

 int main(){
     scanf("%d",&T);
     for (int tt=;tt<=T;tt++){
         scanf("%lld%lld%lld%lld%lld",&p,&a,&b,&x,&t);
         if (x==t) {
             puts("");
         }else{
             if (a==) {
                 printf("%d\n",b==t ?  : -);
             }
             if (a==) {
                 printf("%lld\n",b== ? - : (t-x+p)%p*Q_pow(b,p-,p)%p+);
             }
             if (a>=){
                 LL inv=Q_pow(a-,p-,p);
                 b=b*inv%p;
                 t=(t+b)%p;
                 x=(x+b)%p;
                 t=t*Q_pow(x,p-,p)%p;
                 printf("%lld\n",BSGS(a,t,p)+);
             }
         }
     }
     return ;
 }