P4013 数字梯形问题

\(\color{#0066ff}{题目描述}\)

给定一个由 \(n\) 行数字组成的数字梯形如下图所示。

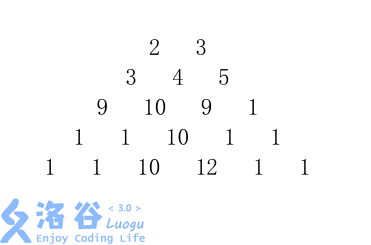
梯形的第一行有 \(m\) 个数字。从梯形的顶部的 \(m\) 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

1.从梯形的顶至底的 \(m\) 条路径互不相交；

2.从梯形的顶至底的 \(m\) 条路径仅在数字结点处相交；

3.从梯形的顶至底的 \(m\) 条路径允许在数字结点相交或边相交。

\(\color{#0066ff}{输入格式}\)

第 \(1\) 行中有 \(2\) 个正整数 \(m\) 和 \(n\)，分别表示数字梯形的第一行有 \(m\) 个数字，共有 \(n\) 行。接下来的 \(n\) 行是数字梯形中各行的数字。

第 \(1\) 行有 \(m\) 个数字，第 \(2\) 行有 \(m+1\) 个数字，以此类推。

\(\color{#0066ff}{输出格式}\)

将按照规则 \(1\)，规则 \(2\)，和规则 \(3\) 计算出的最大数字总和并输出，每行一个最大总和。

\(\color{#0066ff}{输入样例}\)

2 5
2 3
3 4 5
9 10 9 1
1 1 10 1 1
1 1 10 12 1 1

\(\color{#0066ff}{输出样例}\)

66
75
77

\(\color{#0066ff}{数据范围与提示}\)

\(1\leq m,n\leq 20\)

\(\color{#0066ff}{题解}\)

把点权转成边权，每个位置拆点

第一问，所有容量均为1，这样都不会重复

x流到y'，让y'连向y，这样进行下次流动

每一个点向下一层到的点连边，最后一层向终点连边

第二问，因为点可以重复，要考虑终点！！！

把x'到x的边改成inf，这样每个点可以接受来自上面多个点的流

还要把连向t的流改成inf，终点位置可能重合！

第三问，中间的所有边改成inf就行，因为终究还是m条路，所以起点的连边还是1

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#define _ 0
#define LL long long
inline LL in() {
    LL x = 0, f = 1; char ch;
    while (!isdigit(ch = getchar())) (ch == '-') && (f = -f);
    while (isdigit(ch)) x = x * 10 + (ch ^ 48), ch = getchar();
    return x * f;
}
const int maxn = 105000;
struct node {
    int to, dis, can;
    node *nxt, *rev;
    node(int to = 0, int dis = 0, int can = 0, node *nxt = NULL) : to(to), dis(dis), can(can), nxt(nxt) {}
};
const int inf = 0x7fffffff;
int n, m, s, t, cnt;
std::queue<int> q;
typedef node *nod;
nod head[maxn], road[maxn];
bool vis[maxn];
int dis[maxn], change[maxn], mp[505][550], id[550][505];
inline void add(int from, int to, int can, int dis) {
    nod o = new node(to, dis, can, head[from]);
    head[from] = o;
}
inline void link(int from, int to, int can, int dis) {
    add(from, to, can, dis);
    add(to, from, 0, -dis);
    head[from]->rev = head[to];
    head[to]->rev = head[from];
}
inline bool spfa() {
    for (int i = s; i <= t; i++) dis[i] = -inf, change[i] = inf;
    dis[s] = 0;
    q.push(s);
    while (!q.empty()) {
        int tp = q.front();
        q.pop();
        vis[tp] = false;
        for (nod i = head[tp]; i; i = i->nxt) {
            if (dis[i->to] < dis[tp] + i->dis && i->can > 0) {
                dis[i->to] = dis[tp] + i->dis;
                change[i->to] = std::min(change[tp], i->can);
                road[i->to] = i->rev;
                if (!vis[i->to])
                    vis[i->to] = true, q.push(i->to);
            }
        }
    }
    return change[t] != inf;
}
inline int mcmf() {
    int flow = 0, cost = 0;
    while (spfa()) {
        flow += change[t];
        cost += change[t] * dis[t];
        for (int i = t; i != s; i = road[i]->to) {
            road[i]->can += change[t];
            road[i]->rev->can -= change[t];
        }
    }
    return cost;
}
inline void partone() {
    for (int i = 1; i <= m; i++) link(s, id[1][i], 1, mp[1][i]);
    for (int i = 1; i <= m + n - 1; i++) link(id[n][i] + cnt, t, 1, 0);
    for (int i = 1; i <= cnt; i++) link(i + cnt, i, 1, 0);
    for (int i = 1; i <= n - 1; i++)
        for (int j = 1; j <= m + i - 1; j++)
            link(id[i][j], id[i + 1][j] + cnt, 1, mp[i + 1][j]),
                link(id[i][j], id[i + 1][j + 1] + cnt, 1, mp[i + 1][j + 1]);
    printf("%d\n", mcmf());
}
inline void parttwo() {
    for (int i = s; i <= t; i++) head[i] = NULL;
    for (int i = 1; i <= m; i++) link(s, id[1][i], 1, mp[1][i]);
    for (int i = 1; i <= m + n - 1; i++) link(id[n][i] + cnt, t, inf, 0);
    for (int i = 1; i <= cnt; i++) link(i + cnt, i, inf, 0);
    for (int i = 1; i <= n - 1; i++)
        for (int j = 1; j <= m + i - 1; j++)
            link(id[i][j], id[i + 1][j] + cnt, 1, mp[i + 1][j]),
                link(id[i][j], id[i + 1][j + 1] + cnt, 1, mp[i + 1][j + 1]);
    printf("%d\n", mcmf());
}
inline void partthree() {
    for (int i = s; i <= t; i++) head[i] = NULL;
    for (int i = 1; i <= m; i++) link(s, id[1][i], 1, mp[1][i]);
    for (int i = 1; i <= m + n - 1; i++) link(id[n][i] + cnt, t, inf, 0);
    for (int i = 1; i <= cnt; i++) link(i + cnt, i, inf, 0);
    for (int i = 1; i <= n - 1; i++)
        for (int j = 1; j <= m + i - 1; j++)
            link(id[i][j], id[i + 1][j] + cnt, inf, mp[i + 1][j]),
                link(id[i][j], id[i + 1][j + 1] + cnt, inf, mp[i + 1][j + 1]);
    printf("%d\n", mcmf());
}
int main() {
    m = in(), n = in();
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m + i - 1; j++) mp[i][j] = in(), id[i][j] = ++cnt;
    s = 0, t = (cnt << 1) + 1;
    partone(), parttwo(), partthree();
    return 0;
}

好像突然清真了。。。