机器学习（二十四）— 偏差Bias 与方差Variance

1、首先 Error = Bias + Variance 

　　Error反映的是整个模型的准确度，

　　Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，

　　Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

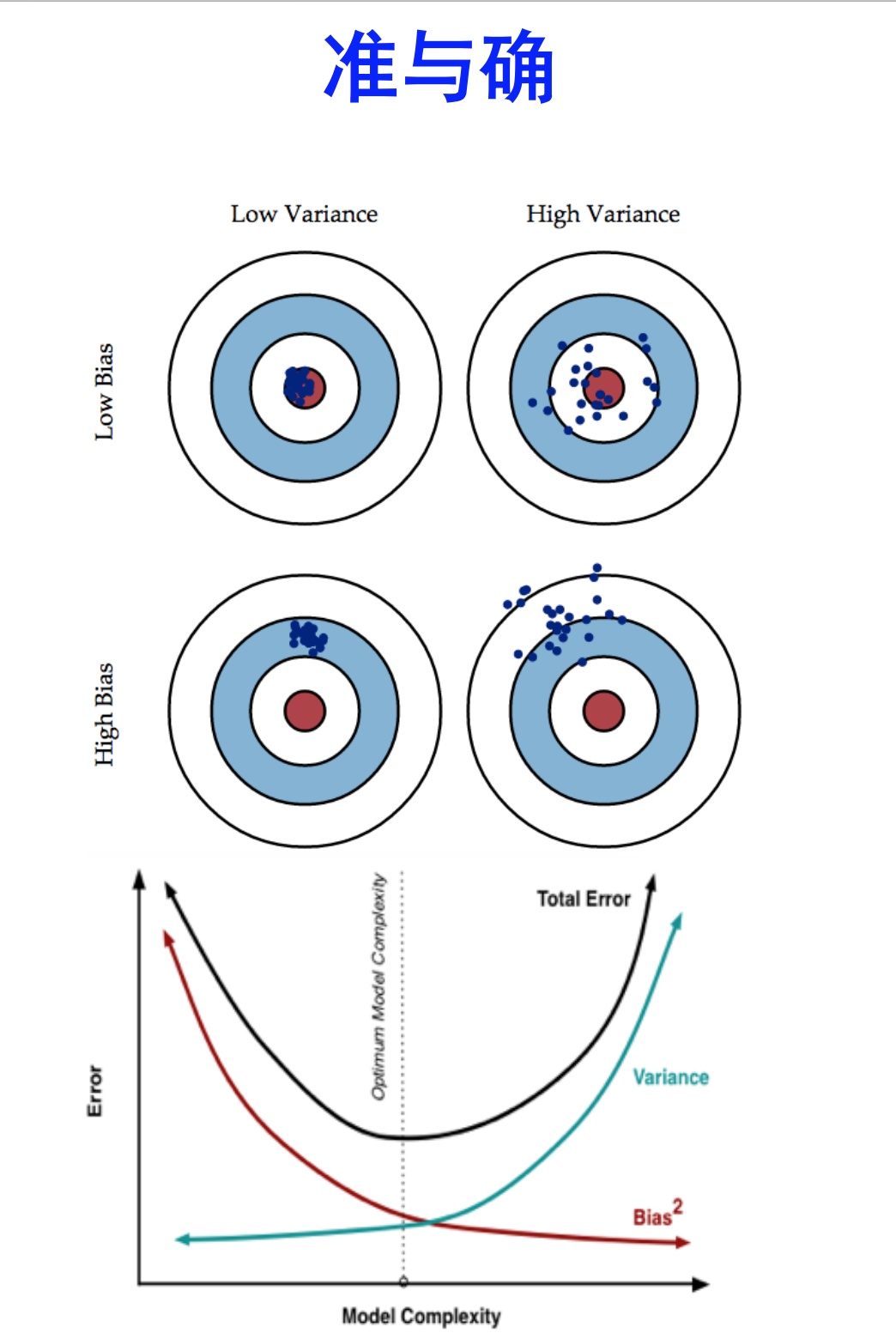
2、Bias与Variance往往是不能兼得的 

　　在一个实际系统中，Bias与Variance往往是不能兼得的。如果要降低模型的Bias，就一定程度上会提高模型的Variance，反之亦然。

　　造成这种现象的根本原因是，我们总是希望试图用有限训练样本去估计无限的真实数据。当我们更加相信这些数据的真实性，而忽视对模型的先验知识，就会尽量保证模型在训练样本上的准确度，这样可以减少模型的Bias。但是，这样学习到的模型，很可能会失去一定的泛化能力，从而造成过拟合，降低模型在真实数据上的表现，增加模型的不确定性。相反，如果更加相信我们对于模型的先验知识，在学习模型的过程中对模型增加更多的限制，就可以降低模型的variance，提高模型的稳定性，但也会使模型的Bias增大。Bias与Variance两者之间的trade-off是机器学习的基本主题之一，可以在各种机器模型中发现它的影子。