机器学习：衡量线性回归法的指标（MSE、RMSE、MAE、R Squared）

一、MSE、RMSE、MAE

• 思路：测试数据集中的点，距离模型的平均距离越小，该模型越精确
• # 注：使用平均距离，而不是所有测试样本的距离和，因为距离和受样本数量的影响

　

　1）公式：

• MSE：均方误差
• 
• RMSE：均方根误差
• 
• MAE：平均绝对误差
• 

二、具体实现

　1）自己的代码

• import numpy as np
  from sklearn.metrics import r2_score
  
  class SimpleLinearRegression:
  
      def __init__(self):
          """初始化Simple Linear Regression模型"""
          self.a_ = None
          self.b_ = None
  
      def fit(self, x_train, y_train):
          """根据训练数据集x_train, y_train训练Simple Linear Regression模型"""
          assert x_train.ndim == 1, \
              "Simple Linear Regressor can only solve single feature training data."
          assert len(x_train) == len(y_train), \
              "the size of x_train must be equal to the size of y_train"
  
          x_mean = np.mean(x_train)
          y_mean = np.mean(y_train)
  
          self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
          self.b_ = y_mean - self.a_ * x_mean
  
          return self
  
      def predict(self, x_predict):
          """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
          assert x_predict.ndim == 1, \
              "Simple Linear Regressor can only solve single feature training data."
          assert self.a_ is not None and self.b_ is not None, \
              "must fit before predict!"
  
          return np.array([self._predict(x) for x in x_predict])
  
      def _predict(self, x_single):
          """给定单个待预测数据x，返回x的预测结果值"""
          return self.a_ * x_single + self.b_
  
      def score(self, x_test, y_test):
          """根据测试数据集 x_test 和 y_test 确定当前模型的准确度：R^2"""
  
          y_predict = self.predict(x_test)
          return r2_score(y_test, y_predict)
  
      def __repr__(self):
          return "SimpleLinearRegression()"

　2）调用scikit-learn中的算法

• from sklearn.metrics import mean_squared_error
  from sklearn.metrics import mean_absolute_error
  
  # MSE
  mse_predict = mean_squared_error(y_test, y_predict)
  
  # MAE
  mae_predict = mean_absolute_error(y_test, y_predict)
  
  # y_test：测试数据集中的真实值
  # y_predict：根据测试集中的x所预测到的数值

　3）RMSE和MAE的比较

1. 量纲一样：都是原始数据中y对应的量纲
2. RMSE > MAE：

　　　# 这是一个数学规律，一组正数的平均数的平方，小于每个数的平方和的平均数；

四、最好的衡量线性回归法的指标：R Squared

• 准确度：[0, 1]，即使分类的问题不同，也可以比较模型应用在不同问题上所体现的优劣；
• RMSE和MAE有局限性：同一个算法模型，解决不同的问题，不能体现此模型针对不同问题所表现的优劣。因为不同实际应用中，数据的量纲不同，无法直接比较预测值，因此无法判断模型更适合预测哪个问题。
• 方案：将预测结果转换为准确度，结果都在[0, 1]之间，针对不同问题的预测准确度，可以比较并来判断此模型更适合预测哪个问题；

　1）计算方法

　

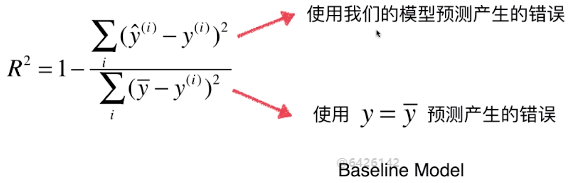
　2）对公式的理解

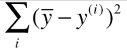• ：公式样式与MSE类似，可以理解为一个预测模型，只是该模型与x无关，在机器学习领域称这种模型为基准模型（Baseline Model），适用于所有的线型回归算法；
• 基准模型问题：因为其没有考虑x的取值，只是很生硬的以为所有的预测样本，其预测结果都是样本均值

　　A）因此对公式可以这样理解：

1. 分子是我们的模型预测产生的错误，分母是使用y等于y的均值这个模型所产生的错误
2. 自己的模型预测产生的错误 / 基础模型预测生产的错误，表示自己的模型没有拟合住的数据，因此R²可以理解为，自己的模型拟合住的数据

　　B）公式推理结论：

1. R² <= 1
2. R²越大越好，当自己的预测模型不犯任何错误时：R² = 1
3. 当我们的模型等于基准模型时：R² = 0
4. 如果R² < 0，说明学习到的模型还不如基准模型。  # 注：很可能数据不存在任何线性关系

　3）公式变形

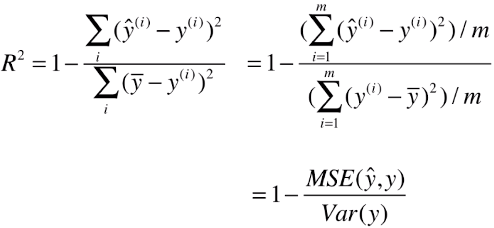
• R²背后具有其它统计意思

　4）R²的代码实现及使用

• 具体代码：

  1 - mean_squared_error(y_true, y_predict) / np.var(y_true)
  
  # mean_squared_error()函数就是MSE
  # np.var(array)：求向量的方差

• 调用scikit-learn中的r2_score()函数：

  from sklearn.metrics import r2_score
  
  r2_score(y_test, y_predict)
  
  # y_test ：测试数据集中的真实值
  # y_predict：预测到的数据